Author Archives: Automated Transfer Script

A2L Item 215

Goal: Relate flux and electric field

Source: 283-405 If phi = 0, is E=0?

True or False: If the electric flux = 0 over some closed Gaussian
surface, then this means that the electric field = 0 on that surface.

  1. True
  2. False

Commentary:

Answer

(2) A good followup question is; Even though the electric field is not
zero everywhere, can it be zero somewhere on the Gaussian surface? If
so, draw a charge configuration for which this is true?

A2L Item 213

Goal: Reasoning regarding electric fields due to distributed charges

Source: 283-395 Electric field from a rod, on its axis.

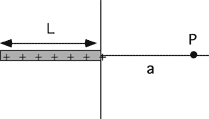
A rod of length L and charge +q
(uniformly distributed) is positioned along the x-axis, as shown to the
right. What is E at point P, a distance a from the origin?

1.

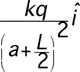2.

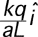3.

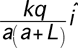4.

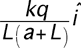5.

Commentary:

Answer

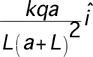(3) It is worthwhile having students examine their choice for the
limiting case a->0. Students are inclined to immediately start a formal
calculation rather than think about the problem long enough to figure
out what they really need to know. In this case all but two of the
answers can be ruled out because they do not limit appropriately as the
point P moves toward the origin. If a>>L the field should drop off as
from a point charge. The only answer meeting both these requirements is
3.

A2L Item 214

Goal: Hone the concept of flux

Source: 283-400, Flux in and out of a balloon.

We construct a closed Gaussian surface in the shape of a sphericalWe construct a closed Gaussian surface in the shape of a spherical
balloon. Assume that a small glass bead with total charge Q is in the
vicinity of the balloon. Consider the following statements:

  1. If the bead is inside the balloon, the electric flux over the
    balloon’s surface can never be 0.

  2. If the bead is outside the balloon,
    the electric flux over the balloon surface must be 0.

Which of these statements is valid?

  1. Only A is valid.
  2. Only B is valid.
  3. Both A and B are valid.
  4. Neither one is valid.

Commentary:

Answer

(3) Students may accept statement A but still think that the value of
the flux depends upon location of the bead in the sphere. Transition
from just inside to just outside poses particular difficulty to some
students. This usually derives from lack of experience with vectors and
dot products. Having the student draw field lines does help, but only
after they comprehend that the formal definition of flux is equivalent
to counting the net number of lines of E crossing the surface.

A2L Item 212

Goal: Reason with electric fields

Source: 283-370 E due to circular rods

All of the curved charged rods shown in the image below have the same
radius and linear charge density (though some are positively charged and
others are negatively charged). For which configuration would the
magnitude of E at the origin be greatest?

Commentary:

Answer

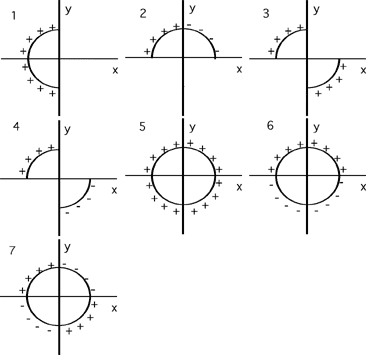
(6) This problem constitutes a good exercise for students learning the
vector nature of the electric field. There are many good followup
questions, such as; Which configurations have zero field at the origin?,
Order the configurations by increasing magnitude of electric field at
the origin. Stress the value of symmetry for reasoning to the answer. A
negative distribution in a quadrant is equivalent to a positive
distribution in the opposite quadrant, which means that distributions #5
and #7 are equivalent (for purposes of finding the E field at the
origin).

A2L Item 210

Goal: Relate representations

Source: 283-342 Graph Ex(x)

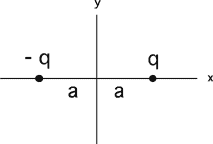
We have a charge configuration
(shown at the right). Which graph is the plot of Ex(x), the
x component of the electric field, as you move along the
x-axis?

Commentary:

Answer

(6) Students should recognize that the field goes singular at the
charges. The only graphs doing that, #1 and #4, are eliminated because
the x-component of the field must be negative everywhere between the two
charges. Have students sketch the graph.

A2L Item 211

Goal: Problem solving with rotational kinematics

Source: CT151.2S02-39

Two masses, attached to the ends of a rigid massless rod, are rotating
about pivot P as shown in the picture below. The mass two meters from P
has speed 0.5m/s. What is the acceleration of the mass one meter from
P?

  1. 0.05 m/s2
  2. 0.0625 m/s2
  3. 0.125 m/s2
  4. 0.250 m/s2
  5. 0.5 m/s2
  6. 1 m/s2
  7. None of the above
  8. Cannot be determined

Commentary:

Answer

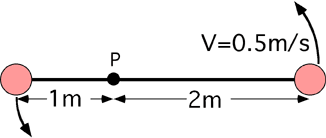
(2) Every one of the possible wrong responses indicates a common error
that students make. After the problem has been discussed it is useful to
have students find the acceleration of the mass at 2m and see that the
accelerations are in the same ratio as the velocities. Drawing vector
diagrams showing the Δv for each mass is useful for explaining this
relationship.

A2L Item 209

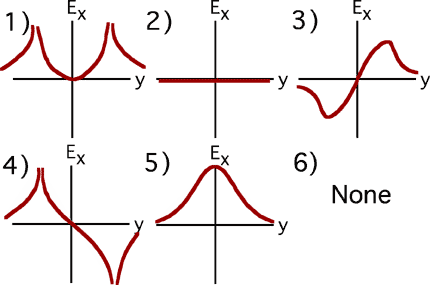
Goal: Translate among representations

Source: 283-341 graph Ex(y)

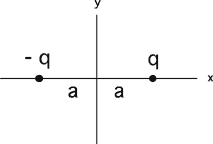
We have a charge configuration
(shown at the right). Which graph below resembles the plot of the x
component of the electric field, Ex(y), as you move
along the y-axis?

Commentary:

Answer

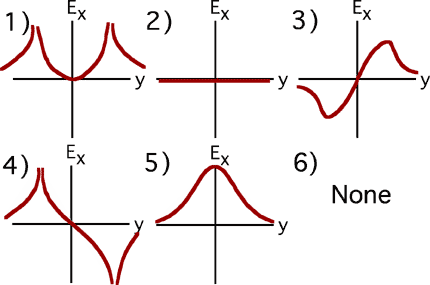
(6) The correct graph looks like the negative of graph #5. Some students
pick #5 thinking that the magnitude of the field is desired.

A2L Item 208

Goal: Hone the concept of electric field

Source: 283-340 Where is E zero near a dipole? 9/21

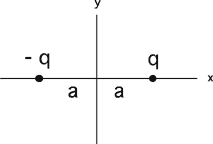
Where,
other than at infinity, is the electric field 0 in the vicinity of the
dipole shown?

  1. Along the y-axis.
  2. At the origin.
  3. At two points, one to the right of (a, 0), the other to the left of (-a,
    0).
  4. At two points on the y-axis, one below the origin, one above the origin.
  5. None of the above.

Commentary:

Answer

(5) Students have a lot of difficulty distinguishing electric field from
potential. Students already exposed to the concept of potential
frequently respond that the field is zero along the y-axis. If there are
many confused students, before identifying the correct response, it
helps to have the students draw the field lines.

A2L Item 206

Goal: Reason regarding induced charges and fields

Source: 283-235 Induced charge in conductors

A positive charge per unit area σ is placed on a cylindrical
conductor of inner radius, r = a, and outer radius, r = b. A positive
charge per unit length, λ, is placed along the axis of the
cylinder. What is the charge density (charge per area) on the outer
surface?

  1. +λ
  2. +σ
  3. -λ
  4. -σ
  5. σ+λ/(2πa)
  6. σ-λ/(2πa)
  7. σ+λ/(2πb)
  8. σ-λ/(2πb)
  9. None of the above

Commentary:

Answer

(7) The biggest problem for students is finding the induced surface
charge density due to the line charge density.

A2L Item 207

Goal: Hone the conservative nature of the electrostatic field

Source: 283-240 Work moving charge around

Two point charges are fixed on the x-axis. A positive charge from point
P to the origin along the different paths shown in the diagram below.
For which path would you do the most work?

  1. Path A
  2. Path B
  3. Path C
  4. Path D
  5. Cannot be determined
  6. None of the above

Commentary:

Answer

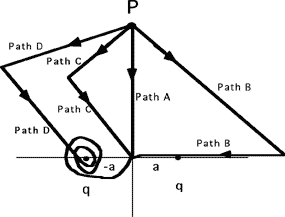
(6) Relating the work done to the change in potential should be
stressed. Once this point is made, a good follow-up question is to ask
how much work would be done if one of the charges on the x-axis was
negative.