Goal: Reasoning with thermodynamics
Source: UMPERG-ctqpe212
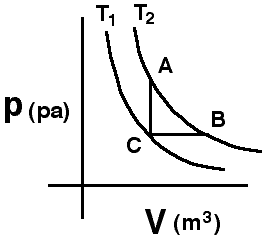
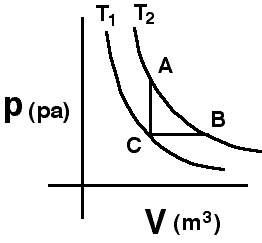
The
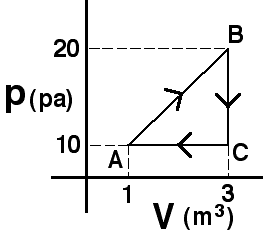
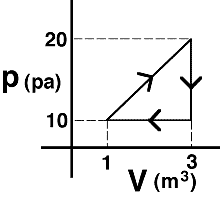
two curves shown are isotherms. A system is taken from state A to state
B along the T2 isotherm. State C has the volume of state A
and the pressure of state B.
Which of the following is true:
Goal: Reasoning with thermodynamics
Source: ctqpe214
A
system consisting of a quantity of ideal gas has the two isotherms
shown. The system, initially at state C, can be taken along path CA to
final state A or along path CB to state B.
Which of the following is true:
(1) Since the internal energy of an ideal gas depends only on
temperature, states A and B have the same internal energy. Along path CB
the system does work requiring more heat to be added than along path CA.
Goal: Problem solving in thermodynamics
Source: UMPERG-ctqpe198
An
amount of an ideal gas is taken around the process shown.The amount of
heat extracted during process BC is
(4) Since no work is done the change in internal energy must be
due to heat extraction. Some students may think that the answer cannot
be determined because they do not know the number of moles. These are
likely thinking that they need to find the temperature at each state to
answer the question.
Goal: Reason with internal energy
Source: UMPERG-ctqpe194var
An
amount of an ideal gas is taken around the process shown. Which of the
following statements about the internal energy of the states is true?
(1) Students need to know only that the internal energy depends
upon the product of p and V. Alternatively, they can reason that,
according to the Ideal Gas Law, this product is proportional to the
temperature and the temperature determines the internal energy
Goal: Link representations
Source: UMPERG-ctqpe196
A vertical cylinder with a movable cap is cooled. The process
corresponding to this is
(4) Interpreting process diagrams is a very important skill for
students. good followup questions include; Is work done during this
process? … by or on the gas? How does the temperature at A compare to
that at C? How much heat was extracted during this process?
Goal: Hone the concept of work for a thermodynamic system
Source: UMPERG-ctqpe190
An
ideal gas is taken around the process shown. The net work done
on the gas is most nearly…
(4) The work done ON the system is the negative of the area of
the triangle. Students selecting answer #1 or #3 need to be sensitized
to the difference between work done on the gas versus by the gas.
Goal: Problem solving with dynamics
Source: UMPERG-ctqpe168
A
uniform disk with mass M and radius R rolls without slipping down an
incline 30° to the horizontal. The friction force acting through
the contact point is
(4) This problem requires students to use the 2nd law written in
terms of the CM acceleration and the rotational dynamic relation written
about the CM or the contact point. In either case they also need the
geometric constraint for rolling. This is a difficult problem for
students requiring a lot of additional knowledge, such as the moment of
inertia for a disk and, depending upon solution method, the Parallel
Axis Theorem.
Having gone to the trouble of solving the problem it is best to make
sure that the students glean as much as they can. A good followup
question is which would have a larger friction force, a hoop, a disk or
a sphere. They may try to reason from the acceleration of these objects
that the larger the acceleration, the smaller the friction force. The
friction force depends upon the mass, however, and the question cannot
be answered without knowledge of the masses.
Goal: Problem solving
Source: UMPERG-ctqpe160
A
uniform disk with R=0.2m rolls without slipping on a horizontal surface.
String is pulled in the horizontal direction with force 15N. Moment of
inertia of disk is 0.4 kg-m2. The acceleration of the center
of the disk is most nearly
(2) This problem can be done without knowing anything about the
friction force. To do so, though, requires knowing the Parallel Axis
Theorem for moments of inertia and the constraint between the linear and
rotational rates of motion for a rolling object. An alternate method is
to write the two equations for the linear motion of the center of mass
and the torque relation for rotation about the CM and then eliminate the
friction from the two equations.
Goal: Problem solving with rotational dynamics
Source: UMPERG-ctqpe167
A
uniform disk with mass M and radius R rolls without slipping down an
incline 30° to the horizontal. The acceleration of the center of
the disk is
(5) The acceleration must be smaller than for a mass sliding on a
frictionless incline, but larger than for a hoop. Application of the
rotational dynamic relation τ = Ipαp about point P, the disk’s contact
point with the incline yields an acceleration of g/3. Students must know
the moment of inertia of the disk about its center and use the Parallel
Axis Theorem.
Good discussion questions are: Would a marble have a larger or smaller
acceleration than a coin? Would the angle of the incline matter?
Goal: Problem solve with rotational dynamics
Source: UMPERG-ctqpe156
A
uniform rod is hinged to a wall and held at a 30° angle by a thin
string that is attached to the ceiling and makes a 90° angle to rod.
The tension in the string is 10N. The weight of the rod is about
(4) Some students will use the wrong trigometric function and
conclude that the weight is 40N.
An interesting follow up question is to ask what is the hinge force.
Students often forget that both the sum of the forces and the sum of the
torques must be zero for static equilibrium.
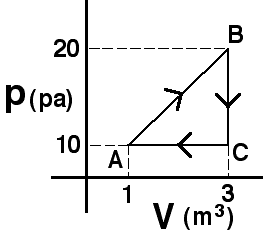
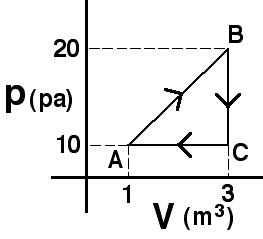
Commentary:
Answer
(5) This is the only answer that is definitely correct. Students
will likely assume that the system is an ideal gas. Many will choose #3
and this should engender a discussion of the sign of work. Physicists
use the convention that positive work is that done BY the system.
Chemists frequently use the opposite convention.
The one choice giving students the most reasoning difficulty is #4. A
reasoning path that eliminates that choice is as follows. Q(AB) is
positive: gas does positive work on surroundings, so heat has to be
added to keep energy the same. Q(CA) is positive: no work is done, so
heat has to be added to raise the temperature. Q (CB) is positive: heat
must be added to expand the gas and still maintain constant pressure. So
Q(CB) [constant pressure] > Q(CA) [constant volume]; Q(CA) – Q(CB) < 0
cannot equal Q(AB) > 0