Goal: Problem solving
Source: UMPERG-ctqpe147
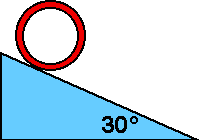
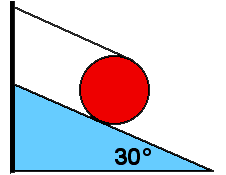
A hoop of mass 4 kg and radius r rolls
without slipping down an incline 30° to the horizontal. The hoop is
released from rest. What is the speed of the hoop after its center has
fallen a distance h?
Goal: Reason with rotational dynamics.
Source: UMPERG-ctqpe138
A spool has string wrapped around its center axle and is sitting on a
horizontal surface. If the string is pulled at an angle to the
horizontal when drawn from the bottom of the axle, the spool will
(4) The motion of the spool depends upon the angle θ. When the line of
action of the force passes through the contact point the spool will
slide and not rotate. At lower angles it will roll to the right and at
higher angles it will roll to the left.
Goal: Hone the concept of torque
Source: UMPERG-ctqpe131
Which of the following statements is true about this situation?
(3) Many students realize that there is at least one point, the
intersection of the lines of action of the two forces, having zero
torque. A drawing is usually sufficient to convince students that there
is an entire line along which the torque is zero.
Goal: Reason with rotational dynamics.
Source: UMPERG-ctqpe136
A spool has string wrapped around its center axle and is sitting on a
horizontal surface. If the string is pulled in the horizontal direction
when tangent to the top of the axle, the spool will
(1) For many students this remains counterintuitive.
Goal: Reason with rotational dynamics.
Source: UMPERG-ctqpe137
A spool has string wrapped around its center axle and is sitting on a
horizontal surface. If the string is pulled in the horizontal direction
when tangent to the bottom of the axle, the spool will
(1) For many students this is really counterintuitive.
Goal: Reasoning about work and energy.
Source: UMPERG-ctqpe72
Consider the two situations shown above. The springs are identical and
are compressed the same amount, but the masses are different with M > m.
The surfaces they sit on have the same non-zero coefficient of friction.
Both start from rest. Which mass has the largest speed when the spring
reaches its relaxed length?
(1) Friction is only a confounding element. The lighter mass will have
the greater speed whether or not there is friction.
Students may correctly reason that the friction force will be less on m
and less of the potential energy stored in the spring will be dissipated
as the spring returns to its relaxed length. While true this is not
relevant for the question.
This is an instance where it is important to elicit student reasoning.
It is a case where students can use wrong reasoning to get the correct
answer.
Goal: Reasoning about forces and torques.
Source: UMPERG-ctqpe158
A uniform rod is hinged to a wall and held at a 30° angle by a thin
string that is attached to the ceiling and makes a 90° angle to rod.
Which statement must be true?
(4) This is easily determined by considering torques about the hinge.
The hinge force cannot be purely vertical because there is a horizontal
component to the tension that must be balanced. Also the hinge force
cannot be purely horizontal or the rod would rotate counterclockwise
about its center. Since the hinge force must have a horizontal component
in the opposite direction as the horizontal component of the tension,
(3) cannot be true either.
Goal: Hone the concept of torque.
Source: UMPERG-ctqpe150
A uniform rod of length L, mass M, is suspended by two thin strings.
Which of the following statements is true regarding the tensions in the
strings?
(3) The ratio is most easily found by considering torques about the
center of the bar. The distances of the strings to the center of the
bar need to be determined visually from the figure.
Goal: Reasoning with forces
Source: UMPERG-ctqpe154
A uniform rod of length 4L, mass M, is suspended by two thin strings,
lengths L and 2L as shown. What is the tension in the string at the
left end of the rod?
(2) For many this is straightforward but a few students are confused
about the effect of the unequal lengths of string.
Goal: Problem solving
Source: UMPERG-ctqpe166
A uniform disk with mass M and radius R sits at rest on an incline
30° to the horizontal. A string is wound around disk and attached
to top of incline as shown. The string is parallel to incline. The
friction force acting at the contact point is:
(3) Balancing torques about the center of the disk determines that the
friction force points up and is equal to the tension in the string. (The
other forces, gravity and normal pass through the point and contribute
no torques.) Balancing torques about the contact point determines the
tension readily.
Commentary:
Answer
(3.) Students should realize that the speed cannot depend upon the
radius. Answer #2 is the speed that a falling point mass would have and
the hoop must have less than that.