Goal: Relate position/time graphs to force.
Source: UMPERG
Position vs. time graphs are given below for four different objects.
Which of the objects experiences a net force sometime during the time
period shown?
Goal: Reason and evaluate statements about a real-world situation.
Source: UMPERG
At the scene of an accident the car causing the crash left skid marks of
a length D. The accident reconstruction team did a test and found that a
police cruiser traveling at the speed limit produces skid marks of
length d < D. Which of the following statements is valid?
(4) is valid assuming that the usual kinetic friction model is
applicable. Some students may think that (3) is valid and indicate (3)
or (5). All of the others are definitely invalid. Since (1) is
invalid, (7) is also invalid.
This question seeks to encourage students to reason and analyze the
situation. It offers the opportunity to engage the students in a
discussion of the meaning of validity as well as the physics underlying
the various assertions.
How would reaction time influence the skid marks?
Suppose the car had several people inside. Would that have affected the
skid marks?
Suppose the test had been made with the same model car as the one in the
accident. Would that make the test more valid?
Allow students to form small groups according to their views and let
them present their arguments to the class. Have student ‘consultants’
suggest appropriate tests to determine if the car was speeding.
Goal: Link energy and kinematic quantities.
Source: UMPERG
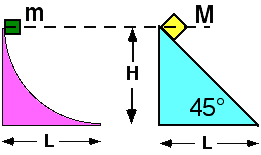
Two masses, m and M, are released from rest at a height H above the
ground. Mass m slides down a curved surface while M slides down an
incline as shown. Both surfaces are frictionless and M > m.
Which of the following statements is true?
(4); even though both blocks arrive at the bottom with the same speed, m
has a larger initial acceleration and attains a larger speed faster than
M, despite having to travel a slightly longer distance. This item helps
to focus attention on identifying those salient characteristics of the
problem that relate to the time it takes the blocks to slide down the
ramps. Some students will cue on the distance traveled, some on the
differing masses of the blocks, some on m picking up speed faster than
M.
The curved surface makes it impossible for students to use either
kinematics or Newton’s Second Law to determine the exact time it takes m
to reach the bottom. Some students may correctly conclude that both
blocks arrive at the bottom with the same speed, and thereby erroneously
conclude that this must mean they arrive at the same time as well.
The curved track case also offers an opportunity to explore whether
students realize that the total work done by the gravitational force
goes into changing the kinetic energy of the block, even with a normal
force present since this normal force does no work on the block.
What features of the problem determine the time it takes the masses to
reach the bottom?
What’s the same about both blocks if they are released from the same
height? What’s different?
Does traveling a shorter distance always mean less time?
For those who answered (1), ask what would happen to the time it would
take M to reach the bottom if the 45° angle were made more, or less
steep (think of the top vertex of the triangle being on a hinge).
Clearly in the limit where M would drop vertically a distance
SQRT(H2+L2), the time it would take to reach the
other vertex of the hypoteneuse would be shorter than for any angle less
than 90°.
Goal: Develop good problem solving practices. Determining the value of procedure forces, those requiring use of the 2nd law.
Source: UMPERG
A child is walking along the sidewalk at a constant speed of 1 m/s while
pulling his dog sitting in a wagon. The dog has a mass of 30kg and the
wagon weighs 50N. If the child pulls the wagon with a force of 60N at an
angle of 30°, what is the frictional force exerted by the wagon on
the dog?
(1) The dog is moving at a constant speed, presumably in a straight
line. The net force on the dog must be zero. Since there are no other
possible horizontal forces (if we ignore air resistance) other than the
friction force, the friction force must be zero.
This problem provides students with a lot of information. The challenge
of the problem (and most real problems) is to come to an understanding
of the situation independent of the specific details. Then based on an
understanding of the situation one can attempt to address specific
questions and make use of detailed information.
Ask students to describe the situation. Ask them to describe how they
approached the problem. Did you describe all the forces? Did you draw
any free-body diagrams?
Have students draw a free-body diagram (drawing all possible forces) for
the dog. Have them describe the motion for the dog. Ask them to
re-answer the question.
Goal: Develop the ability to identify 3rd-Law Pairs, the parts of an interaction.
Source: UMPERG-ctqpe42
The two blocks shown below are identical. In case A the block sits on a horizontal surface and in case B the block is in free fall.
Which of the following statements are true regarding the reaction force to the gravitational force exerted on each block?
(6) The reaction force to the gravitational force exerted (by the
earth) on a block is the gravitational force exerted (by the block) on
the earth. In both cases the reaction force is non zero and because the
blocks are identical the reaction forces for the two cases are
equal.
Newton’s third law can be counter intuitive to many students and the
concept of reaction force can be very confusing. Students often think
that the reaction force to some force exerted on an object is a
balancing force on the same object.
(1) Many students will think the normal force is the reaction force
because it is equal and opposite to the gravitational force exerted on
the block.
(2) Some students may reason that since there is no balancing force
there is no reaction force.
What is a reaction force? What are some examples? Do action-reaction
force pairs act on the same, or different bodies? Why is reaction force
an important idea?
Reaction force is an abstract concept. It cannot be demonstrated. One
needs to make sure students understand its definition. The first step is
to make sure students understand the idea of an interaction: When two
objects affect each other (i.e., influence each others motion, or shape)
then we say that the objects interact. We find that all interactions are
two-way: if the motion/shape of one of the interacting objects is
affected then the motion/shape of the other object is always affected.
We ultimately quantify the effects and refer to the causes of these
effects as forces. An interaction involves two forces, one on each
object. Action-reaction pair refer to the two parts (forces) of an
interaction. Newton’s third law states the relationship between the two
parts (forces) of an interaction: the two forces are equal in magnitude
and point opposite in direction.
Goal: Recognizing how the concept of force relates to interactions.
Source: UMPERG
A bowling ball rolls down an alley and hits a bowling pin. Which
statement below is true about the forces exerted during the impact?
(3); The forces are equal (independent of the masses and motions of the
interacting objects), as required by Newton’s Third Law .
In situations where a heavier, moving object collides with a lighter,
stationary object, students have a very strong intuition that the
heavier, moving object exerts a larger force on the lighter, stationary
object. This intuition is based on experiences like the following: when
a bowling ball hits a pin, the ball continues to move forward and the
pin goes flying off the lane. Students interpret the large change in the
pin’s motion as evidence that the ball (which is heavier than the pin)
exerts a larger force on the pin than vice versa. Often, when a car and
a truck collide, the car suffers much more damage than the truck, and so
students interpret this as evidence that the truck exerts a larger force
on the car. For background reading on helping students overcome this
persistent misconception see Thornton and Sokoloff: Sokoloff, D.R.
& Thornton, R.K. (1997), Using interactive lecture demonstrations to
create an active learning environment, The Physics Teacher, 27, No. 6,
340; and Thornton, R.K. and Sokoloff, D.R. (1998), Assessing student
learning of Newton’s Laws: The force and motion conceptual evaluation
and the evaluation of active learning laboratory and lecture curricula,
American Journal of Physics, 64, 338-352 (1998).
Which object, the bowling ball or the bowling pin, has the larger
acceleration? How do you know?
Which object experiences the larger net force? How do you know?
Would your answer to the original question change if a moving pin hit a
stationary bowling ball?
If you have MBL equipment and force probes, collide a moving cart with a
stationary cart of the same mass. Ask students to compare the forces
exerted on the two carts. Ask students to compare the velocities and
accelerations of the two carts. Repeat using different initial
conditions.
Draw a picture of a large moving cart colliding with a small stationary
cart. Draw a spring between the carts. Ask students how they would
determine the force on each cart given the spring constant and spring
compression.
Take a bathroom scale, place it between two students (a large strong
student and a slight student) and have them push as hard as they can
from either end without making the scale accelerate–observe the scale
reading. Repeat with the scale reversed. Ask if there is much
difference in the scale reading depending on which way the front of the
scale is facing. What does this imply about the forces exerted by the
strong and the slight student on each other?
Goal: Relating physical motion with graphical representation
Source: UMPERG
Which of the velocity vs. time plots shown below might represent the
velocity of a cart projected up an incline?
Select one of the above or:
(7) None of the above
(8) Cannot be determined
(3) or (4). Initially the cart has a non-zero velocity pointing up the
incline. The speed of the cart decreases as it moves up the incline,
reaching zero at its maximum height. The speed of the cart increases as
the cart moves down the incline. The velocity at the bottom of the
incline points down the incline. Graph (3)/(4) is correct if up/down
the incline is taken as the positive direction.
Students will often associate velocity time graphs with features of the
terrain. Many will pick either (5) because they neglect the vector
nature of velocity and think about the speed.
Is the velocity ever zero? Is the velocity ever positive? … negative?
When? Is the velocity constant? How do you know?
Plotting the position vs. time may help students come up with the
correct plot of velocity vs. time.
Goal: Honing the concept of acceleration especially regarding circular motion.
Source: UMPERG
A child is swinging. What is the direction of her acceleration when the
swing is at its lowest point?
(1) The acceleration is in the upward direction. The child is traveling
in a circle and at the lowest point the acceleration is all radial.
Circular motion must have been covered for the item to be of use. The
question may be answered using either kinematics or dynamics. The
direction of the acceleration can be realized using kinematics by
drawing the velocity vector just before the lowest point and just after
the lowest point. The difference is proportional to the acceleration
and this difference points toward the center of the circle. At the
lowest point all forces are vertical so the acceleration must also be in
the vertical direction. The tension is larger than the weight so the
acceleration is in the upward direction.
What is the definition of acceleration? What is the direction of the
velocity of the child when at the lowest point of the swing? Is it
getting larger or smaller? Is it changing direction? What forces act
on the child at the lowest point of the swing and in what direction are
these forces?
Have students draw a motion plot indicating the position and the
velocity vector of the child at various points in the child’s motion.
Do their drawings reflect that the velocity is always tangent to the
circular path, but increasing in magnitude as the child swings toward
the lowest point?
Goal: Relating physical understanding of an object’s behavior to a graphical representation of acceleration.
Source: UMPERG
A soccer ball rolls across the road and down a hill as shown below. At
the bottom of the hill the ball is given a quick kick so that the ball
goes back up the hill and across the road. The initial and final speed
of the ball is the same.
Which of the following sketches of ax vs. t is a reasonable
representation of the horizontal acceleration of the ball as a function
of time for period of time shown?
(2) The acceleration of the ball while on the slope is the same whether
it is going down or going up. Also, taking the positive direction to
the right, the kick would appear as a negative spike in the
acceleration.
This item is related to item 1. See comments there. Students need to
note that the plots are for the xcomponent of the acceleration.
How is the acceleration related to the velocity? Suppose the hill were
more inclined. What feature of the acceleration vs. time graph would
change? What is the direction of the velocity just before the kick?
just after?
Have students make a graph of velocity vs. time for each of the given
plots of acceleration vs. time. Have students generate a plot of the
acceleration and velocity in the y direction.
Goal: Differentiate between magnitude and direction of acceleration.
Source: UMPERG
| Case | Column 1 | Column 2 |
| (A) | A car goes from 0 to 60 mph in 6s along a straight highway. |
A car goes from 60 to 0 mph in 6s along a straight highway. |
| (B) | A race car travels around a circular track at 50 mph. |
A race car travels around the same circular track at 100 mph. |
| (C) | A ball is thrown straight up. It rises 20 ft. Ignore the effects of the air. |
A ball is dropped straight down. It falls 20 ft. Ignore the effects of the air. |
For which cases is the acceleration the same for the motion described
in both columns?
(3) The only case having the same acceleration is C where the
acceleration is that due to the gravitational force. In case A, the
magnitude of the two accelerations is the same but one is positive and
the other negative, i.e. the vectors point in opposite directions.
[This assumes that the acceleration is uniform.] In case B, the
“direction” is the same, i.e. pointing toward the center of the circle,
but the magnitudes are different.
This question reveals whether students have the concept of acceleration
as a vector (i.e. has direction as well as magnitude). Some students
may ignore the magnitude completely and key on the direction. The
objective here is to have students indicate the concept of acceleration
that they are using to answer the question.
For which cases is the magnitude of the acceleration the same? the
direction?
For which cases does the acceleration change during the motion
described?
Have students draw a motion diagram (a strobe diagram with the velocity
vector indicated at each position). This diagram helps students to
associate the acceleration with a change in velocity.
Commentary:
Answer
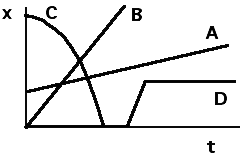
(8) is the appropriate response because both C and D experience a force
during the time interval. A and B have constant velocity because the
slope of their x vs. t plot is constant. Some students may not realize
that D experiences a force because they will reason that D has constant
velocity at any given time. However, D must experience a force to
change its velocity.
Background
Recognizing the signature of acceleration from a plot of position vs.
time is an important skill for students to develop. Because of
familiarity, they may recognize the plot of position for a falling body
and reason that the object experiences a gravitational force. This
question requires two logical steps. First recognizing the consequence
of constant velocity and second recognizing that a change of velocity
indicates acceleration and therefore force.
Questions to Reveal Student Reasoning
Which objects have constant velocity throughout the time interval?
Which of the objects has the largest speed sometime during the time
interval?
Are all of the objects moving away from the origin?
Suggestions
Have students plot the velocity of each object over the same time
interval.
Have students move objects in a manner in accord with the plots. This
may cause them to realize when a force must be applied.