Goal: Honing the idea of constant acceleartion.
Source: UMPERG
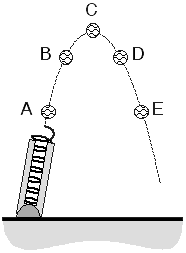
A baseball is shot into the air from a spring loaded cannon. The diagram shows the ball at five locations. At which location is the magnitude of the acceleration least?
Goal: Differentiate velocity and acceleration in the context of free-fall motion.
Source:
A person throws a ball straight up in the air. The ball rises to a maximum height and then falls back down so that the person catches it. Consider the ball while it is in the air.
Which of the following statements are true?
A. Just after the ball leaves the person’s hand the direction of the acceleration is up.
B. The acceleration is zero when the ball reaches its maximum height.
C. The acceleration is about 9.8 m/s2 (down) when the ball is falling.
After the ball leaves the person’s hand, its acceleration is 9.8 m/s2 (down) throughout the entire motion (assuming air resistance can be neglected). Answer (3) is the best choice.
Use this item during kinematics, shortly after the introduction of “acceleration.” We suggest that students have some experience analyzing the velocity of objects undergoing freefall motion. Intended focus: (1) Do students think that the acceleration is zero at the maximum height, where the ball momentarily stops? (2) Do students think that the acceleration points in the same direction as the velocity? (3) Can students apply the definition of acceleration to a familiar situation?
The goal is to have students confront existing misconceptions:1) Students often believe that the acceleration must point in the direction of the motion; and 2) Students often believe that the acceleration is 9.8 throughtout free fall but zero at the top of the trajectory since the vertical speed is zero there.
Have students sketch the velocity of the ball as a function of time. Ask how the acceleration is related to this graph.
Using Microcomputer Based Lab software and a sonic ranger, generate a velocity graph for a cart going up and down an incline. Discuss how the graph relates to a velocity vs. time graph for a ball thrown vertically.
Goal: Hone the concept of acceleration.
Source: UMPERG
HOW MANY of the identified objects are NOT accelerating?
Enter the number of objects, or 8 for “none” and 9 for “cannot be determined”.
Only the skydiver, who has reached terminal velocity, has zero acceleration. In each of the other situations, the acceleration is nonzero because either the speed or the direction of motion is changing. Answer (2) is the best choice.
Context for Use: Give after introducing the concept of acceleration. Intended focus: What factors/criteria do students use to determine whether an object is accelerating? The goal is to focus students on changes in the speed/direction of an object’s motion.
How do you know whether an object is accelerating? What are some examples of objects undergoing acceleration? If an object is falling is it necessarily accelerating?
In some cases did you need to make assumptions before deciding whether the object was accelerating? (Ask students to provide examples.)
Have students write out how they determine whether an object is accelerating. After discussing the different methods, have students vote on which one they think is best.
Play a “challenge game” with the class. Two teams of students think of situations in which an object undergoes some motion. The teams then take turns challenging each other to determine whether or not the objects are accelerating.
Goal: Interrelate representations of acceleration and identifying potential misconceptions.
Source: UMPERG
Which of the following statements are true?
A. While an object moves at constant speed, its acceleration must be zero.
B. For a ball to roll up a hill and then back down, its acceleration must change.
C. When an object’s velocity versus time graph crosses the time axis, its acceleration must be zero.
Answer (8) is the best choice. An object’s acceleration is nonzero if its direction of motion is changing, or its speed is changing, or both. A constant speed does not imply zero acceleration because the object’s direction of motion could be changing. Therefore (A) is false. An object will have a nonzero acceleration if its velocity is changing, even if its velocity is (instantaneously) zero. Therefore (C) is false. For a ball that rolls up a hill and then back down, the acceleration can be constant. This will be the case if the hill has a constant slope, and the friction and air resistance forces are small. Therefore (B) is also false.
Assessment Issues: (1) Do students know that an object has a nonzero acceleration whenever its speed or direction of motion change? Do they think that the speed must change for there to be a nonzero acceleration? (2) Do students confuse velocity and acceleration? Do they think that the acceleration is positive/zero/negative whenever the velocity is positive/zero/negative? (3) Do students use graphs and pictures to answer this question?
Have one group of students perform some motion (perhaps by walking or moving an object), and challenge another group to graph position versus time, velocity versus time, or acceleration versus time for that motion. (If the motion performed is in two dimensions, students should graph one of the components of the motion.)
Goal: Relating physical understanding of an object’s motion to a graphical representation of acceleration.
Source: UMPERG
A soccer ball rolls slowly across the road and down a hill as shown below:
Which of the following sketches of ax vs. t is a reasonable representation of the horizontal acceleration of the ball as a function of time?
We will assume that rolling friction between the ball and road surface is small and that air resistance can be ignored. We will also assume that the ball does not leave the road surface at the top of the hill. If these assumptions are satisfied, the ball will roll across the level road at a (nearly) constant velocity. As it rolls down the hill, the ball will speed up, producing a constant acceleration in the direction of motion. There will be a nonzero component of acceleration pointing to the right. The graph at the right is a reasonable representation of the horizontal acceleration as a function of time. For our assumptions, answer (5) is the best choice.
Context for Use: Give after students explore the vector nature of acceleration. Formal (quantitative) kinematics is not required.
Assessment Issues: (1) Can students recognize when an object is accelerating? What criteria do they use? (2) Do students perceive nonzero horizontal and vertical components of acceleration? Do some students think that the acceleration is in the y-direction only? (3) Do students think that the acceleration graph looks like the sketch of the road on which the ball rolls? What process do they use to construct a graph of acceleration versus time? (4) Do students confuse the different motion quantities? For example, do they interpret the graphs of acceleration versus time as velocity versus time graphs?
Where does the ball speed up? Where does it slow down? Why does its speed change?
What is the direction of the ball’s acceleration while it is on the hill? Does the ball accelerate to the right? Does the ball accelerate vertically?
Help students construct the horizontal (and vertical) velocity vs. time graph for the ball. If students have been exposed to forces, draw a free-body diagram and use it to find the net force.
Commentary:
Answer
The ball’s acceleration is 9.8 m/s2 (down) throughout its
entire motion (assuming air resistance can be neglected). Answer (8) is
the best choice.
Background
Students should have some experience analyzing the velocity of objects
undergoing free-fall motion. Issues to consider: (1) Do students think
that the acceleration is zero at the maximum height, where the ball
momentarily stops? (2) Do students think that the acceleration points
in the same direction as the velocity? (3) Can students apply the
definition of acceleration to a familiar situation?
The goal is to have students confront existing misconceptions: 1)
Students often believe that the acceleration must point in the direction
of the motion; and 2) Students often believe that the acceleration is
9.8 throughout free fall but zero at the top of the trajectory since the
vertical speed is zero there.
Questions to Reveal Student Reasoning
direction of the acceleration? Is the acceleration changing?
direction of the acceleration? Is the acceleration changing?
height? Is the velocity of the ball changing at the maximum height?
Suggestions
Ask students to apply the operational definition of acceleration (take
the velocity vector just after C and subtract the velocity vector just
before C and divide by the time interval). Have them compare the x/y
component of the velocity just before C with the x/y component of the
velocity just after point C.
For students who persist in thinking that both the velocity and
acceleration are zero at the top of a trajectory, contrast the
subsequent motion with that of an object sitting at rest on a surface.