Category Archives: High School

Items appropriate for use in a high school physics course.

A2L Item 022

Goal: Link energy and kinematic quantities.

Source: UMPERG

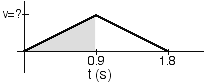
Two masses, m and M, are released from rest at a height H above the
ground. Mass m slides down a curved surface while M slides down an
incline as shown. Both surfaces are frictionless and M > m.

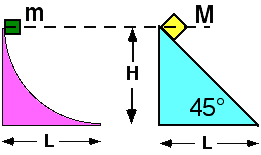
Which of the following statements is true?

  1. The time it takes for m to reach the end of the surface is longer because the path it takes is longer.
  2. The time it takes is the same since both masses are released from the same height.
  3. The time it takes for M to reach the end of the incline is less because its horizontal acceleration is larger.
  4. The time it takes for m to reach the end of the surface is shorter because it has a larger acceleration initially and therefore builds speed more quickly.
  5. The time it takes is the same since both masses have the same displacement.
  6. The time it takes is the same because both masses have the same speed at the end.
  7. The times cannot be compared without knowing the masses of the blocks.
  8. More than one statement above is correct
  9. None of the above statements is correct.

Commentary:

Answer

(4); even though both blocks arrive at the bottom with the same speed, m
has a larger initial acceleration and attains a larger speed faster than
M, despite having to travel a slightly longer distance. This item helps
to focus attention on identifying those salient characteristics of the
problem that relate to the time it takes the blocks to slide down the
ramps. Some students will cue on the distance traveled, some on the
differing masses of the blocks, some on m picking up speed faster than
M.

Background

The curved surface makes it impossible for students to use either
kinematics or Newton’s Second Law to determine the exact time it takes m
to reach the bottom. Some students may correctly conclude that both
blocks arrive at the bottom with the same speed, and thereby erroneously
conclude that this must mean they arrive at the same time as well.

The curved track case also offers an opportunity to explore whether
students realize that the total work done by the gravitational force
goes into changing the kinetic energy of the block, even with a normal
force present since this normal force does no work on the block.

Questions to Reveal Student Reasoning

What features of the problem determine the time it takes the masses to
reach the bottom?

What’s the same about both blocks if they are released from the same
height? What’s different?

Does traveling a shorter distance always mean less time?

Suggestions

For those who answered (1), ask what would happen to the time it would
take M to reach the bottom if the 45° angle were made more, or less
steep (think of the top vertex of the triangle being on a hinge).
Clearly in the limit where M would drop vertically a distance
SQRT(H2+L2), the time it would take to reach the
other vertex of the hypoteneuse would be shorter than for any angle less
than 90°.

A2L Item 023

Goal: Develop good problem solving practices. Determining the value of procedure forces, those requiring use of the 2nd law.

Source: UMPERG

A child is walking along the sidewalk at a constant speed of 1 m/s while
pulling his dog sitting in a wagon. The dog has a mass of 30kg and the
wagon weighs 50N. If the child pulls the wagon with a force of 60N at an
angle of 30°, what is the frictional force exerted by the wagon on
the dog?

  1. 0N
  2. 2N
  3. 5N
  4. 10N
  5. 15N
  6. 20N
  7. 32N
  8. None of the above
  9. Cannot be determined

Commentary:

Answer

(1) The dog is moving at a constant speed, presumably in a straight
line. The net force on the dog must be zero. Since there are no other
possible horizontal forces (if we ignore air resistance) other than the
friction force, the friction force must be zero.

Background

This problem provides students with a lot of information. The challenge
of the problem (and most real problems) is to come to an understanding
of the situation independent of the specific details. Then based on an
understanding of the situation one can attempt to address specific
questions and make use of detailed information.

Questions to Reveal Student Reasoning

Ask students to describe the situation. Ask them to describe how they
approached the problem. Did you describe all the forces? Did you draw
any free-body diagrams?

Suggestions

Have students draw a free-body diagram (drawing all possible forces) for
the dog. Have them describe the motion for the dog. Ask them to
re-answer the question.

A2L Item 021

Goal: Develop the ability to identify 3rd-Law Pairs, the parts of an interaction.

Source: UMPERG-ctqpe42

The two blocks shown below are identical. In case A the block sits on a horizontal surface and in case B the block is in free fall.

Which of the following statements are true regarding the reaction force to the gravitational force exerted on each block?

  1. In case A the reaction force is the Normal force.
  2. In case B the reaction force is zero.
  3. The reaction force is larger in A than B.
  4. All the above are true.
  5. Only (1) & (2) are true.
  6. None of the above are true.
  7. Cannot be determined.

Commentary:

Answer

(6) The reaction force to the gravitational force exerted (by the
earth) on a block is the gravitational force exerted (by the block) on
the earth. In both cases the reaction force is non zero and because the
blocks are identical the reaction forces for the two cases are
equal.

Background

Newton’s third law can be counter intuitive to many students and the
concept of reaction force can be very confusing. Students often think
that the reaction force to some force exerted on an object is a
balancing force on the same object.

(1) Many students will think the normal force is the reaction force
because it is equal and opposite to the gravitational force exerted on
the block.

(2) Some students may reason that since there is no balancing force
there is no reaction force.

Questions to Reveal Student Reasoning

What is a reaction force? What are some examples? Do action-reaction
force pairs act on the same, or different bodies? Why is reaction force
an important idea?

Suggestions

Reaction force is an abstract concept. It cannot be demonstrated. One
needs to make sure students understand its definition. The first step is
to make sure students understand the idea of an interaction: When two
objects affect each other (i.e., influence each others motion, or shape)
then we say that the objects interact. We find that all interactions are
two-way: if the motion/shape of one of the interacting objects is
affected then the motion/shape of the other object is always affected.
We ultimately quantify the effects and refer to the causes of these
effects as forces. An interaction involves two forces, one on each
object. Action-reaction pair refer to the two parts (forces) of an
interaction. Newton’s third law states the relationship between the two
parts (forces) of an interaction: the two forces are equal in magnitude
and point opposite in direction.

A2L Item 020

Goal: Recognizing how the concept of force relates to interactions.

Source: UMPERG

A bowling ball rolls down an alley and hits a bowling pin. Which
statement below is true about the forces exerted during the impact?

  1. The bowling pin exerts a larger force on the ball than the ball does
    on the pin.
  2. The bowling ball exerts a larger force on the pin than the pin does
    on the ball.
  3. The force that they exert on each other is the same size.
  4. One of the two forces is larger, but which is larger can’t be
    determined unless more information is provided.
  5. None of the above.
  6. Cannot be determined

Commentary:

Answer

(3); The forces are equal (independent of the masses and motions of the
interacting objects), as required by Newton’s Third Law .

Background

In situations where a heavier, moving object collides with a lighter,
stationary object, students have a very strong intuition that the
heavier, moving object exerts a larger force on the lighter, stationary
object. This intuition is based on experiences like the following: when
a bowling ball hits a pin, the ball continues to move forward and the
pin goes flying off the lane. Students interpret the large change in the
pin’s motion as evidence that the ball (which is heavier than the pin)
exerts a larger force on the pin than vice versa. Often, when a car and
a truck collide, the car suffers much more damage than the truck, and so
students interpret this as evidence that the truck exerts a larger force
on the car. For background reading on helping students overcome this
persistent misconception see Thornton and Sokoloff: Sokoloff, D.R.
& Thornton, R.K. (1997), Using interactive lecture demonstrations to
create an active learning environment, The Physics Teacher, 27, No. 6,
340; and Thornton, R.K. and Sokoloff, D.R. (1998), Assessing student
learning of Newton’s Laws: The force and motion conceptual evaluation
and the evaluation of active learning laboratory and lecture curricula,
American Journal of Physics, 64, 338-352 (1998).

Questions to Reveal Student Reasoning

Which object, the bowling ball or the bowling pin, has the larger
acceleration? How do you know?

Which object experiences the larger net force? How do you know?

Would your answer to the original question change if a moving pin hit a
stationary bowling ball?

Suggestions

If you have MBL equipment and force probes, collide a moving cart with a
stationary cart of the same mass. Ask students to compare the forces
exerted on the two carts. Ask students to compare the velocities and
accelerations of the two carts. Repeat using different initial
conditions.

Draw a picture of a large moving cart colliding with a small stationary
cart. Draw a spring between the carts. Ask students how they would
determine the force on each cart given the spring constant and spring
compression.

Take a bathroom scale, place it between two students (a large strong
student and a slight student) and have them push as hard as they can
from either end without making the scale accelerate–observe the scale
reading. Repeat with the scale reversed. Ask if there is much
difference in the scale reading depending on which way the front of the
scale is facing. What does this imply about the forces exerted by the
strong and the slight student on each other?

A2L Item 019

Goal: Relating physical motion with graphical representation

Source: UMPERG

Which of the velocity vs. time plots shown below might represent the
velocity of a cart projected up an incline?

Select one of the above or:

(7) None of the above

(8) Cannot be determined

Commentary:

Answer

(3) or (4). Initially the cart has a non-zero velocity pointing up the
incline. The speed of the cart decreases as it moves up the incline,
reaching zero at its maximum height. The speed of the cart increases as
the cart moves down the incline. The velocity at the bottom of the
incline points down the incline. Graph (3)/(4) is correct if up/down
the incline is taken as the positive direction.

Background

Students will often associate velocity time graphs with features of the
terrain. Many will pick either (5) because they neglect the vector
nature of velocity and think about the speed.

Questions to Reveal Student Reasoning

Is the velocity ever zero? Is the velocity ever positive? … negative?
When? Is the velocity constant? How do you know?

Suggestions

Plotting the position vs. time may help students come up with the
correct plot of velocity vs. time.

A2L Item 018

Goal: Honing the concept of acceleration especially regarding circular motion.

Source: UMPERG

A child is swinging. What is the direction of her acceleration when the
swing is at its lowest point?

  1. Up
  2. Down
  3. In the direction of the child’s motion
  4. Opposite the direction of the child’s motion
  5. Zero acceleration, direction can’t be defined.
  6. None of the above
  7. Cannot be determined

Commentary:

Answer

(1) The acceleration is in the upward direction. The child is traveling
in a circle and at the lowest point the acceleration is all radial.

Background

Circular motion must have been covered for the item to be of use. The
question may be answered using either kinematics or dynamics. The
direction of the acceleration can be realized using kinematics by
drawing the velocity vector just before the lowest point and just after
the lowest point. The difference is proportional to the acceleration
and this difference points toward the center of the circle. At the
lowest point all forces are vertical so the acceleration must also be in
the vertical direction. The tension is larger than the weight so the
acceleration is in the upward direction.

Questions to Reveal Student Reasoning

What is the definition of acceleration? What is the direction of the
velocity of the child when at the lowest point of the swing? Is it
getting larger or smaller? Is it changing direction? What forces act
on the child at the lowest point of the swing and in what direction are
these forces?

Suggestions

Have students draw a motion plot indicating the position and the
velocity vector of the child at various points in the child’s motion.
Do their drawings reflect that the velocity is always tangent to the
circular path, but increasing in magnitude as the child swings toward
the lowest point?

A2L Item 017

Goal: Relating physical understanding of an object’s behavior to a graphical representation of acceleration.

Source: UMPERG

A soccer ball rolls across the road and down a hill as shown below. At
the bottom of the hill the ball is given a quick kick so that the ball
goes back up the hill and across the road. The initial and final speed
of the ball is the same.

Which of the following sketches of ax vs. t is a reasonable
representation of the horizontal acceleration of the ball as a function
of time for period of time shown?

Commentary:

Answer

(2) The acceleration of the ball while on the slope is the same whether
it is going down or going up. Also, taking the positive direction to
the right, the kick would appear as a negative spike in the
acceleration.

Background

This item is related to item 1. See comments there. Students need to
note that the plots are for the xcomponent of the acceleration.

Questions to Reveal Student Reasoning

How is the acceleration related to the velocity? Suppose the hill were
more inclined. What feature of the acceleration vs. time graph would
change? What is the direction of the velocity just before the kick?
just after?

Suggestions

Have students make a graph of velocity vs. time for each of the given
plots of acceleration vs. time. Have students generate a plot of the
acceleration and velocity in the y direction.

A2L Item 015

Goal: Differentiate between magnitude and direction of acceleration.

Source: UMPERG

Case Column 1 Column 2
(A) A car goes from 0 to 60 mph in 6s along a
straight highway.		 A car goes from 60 to 0 mph in 6s along a
straight highway.
(B) A race car travels around a circular
track at 50 mph.		 A race car travels around the same circular
track at 100 mph.
(C) A ball is thrown straight up. It rises
20 ft. Ignore the effects of the air.		 A ball is dropped
straight down. It falls 20 ft. Ignore the effects of the
air.

For which cases is the acceleration the same for the motion described
in both columns?

  1. Case A only
  2. Case B only
  3. Case C only
  4. Cases A & B
  5. Cases B & C
  6. Cases A & C
  7. Cases A, B & C
  8. None of the cases
  9. Cannot be determined

Commentary:

Answer

(3) The only case having the same acceleration is C where the
acceleration is that due to the gravitational force. In case A, the
magnitude of the two accelerations is the same but one is positive and
the other negative, i.e. the vectors point in opposite directions.
[This assumes that the acceleration is uniform.] In case B, the
“direction” is the same, i.e. pointing toward the center of the circle,
but the magnitudes are different.

Background

This question reveals whether students have the concept of acceleration
as a vector (i.e. has direction as well as magnitude). Some students
may ignore the magnitude completely and key on the direction. The
objective here is to have students indicate the concept of acceleration
that they are using to answer the question.

Questions to Reveal Student Reasoning

For which cases is the magnitude of the acceleration the same? the
direction?

For which cases does the acceleration change during the motion
described?

Suggestions

Have students draw a motion diagram (a strobe diagram with the velocity
vector indicated at each position). This diagram helps students to
associate the acceleration with a change in velocity.

A2L Item 016

Goal: Differentiate between instantaneous and average acceleration.

Source: UMPERG

Below is shown a strobe diagram indicating the position of four objects
at successive time intervals. The objects move from left to right.

During the intervals shown, which object would you estimate has the
largest average acceleration?

  1. Object A
  2. Object B
  3. Object C
  4. Object D
  5. Objects A, B, & D
  6. Cannot estimate for (A) because its acceleration is changing
  7. Cannot estimate average acceleration from a strobe diagram
  8. None of the above
  9. Cannot be determined

Commentary:

Answer

(3) Assuming that the question is referring to magnitude, the largest
average acceleration is experienced by object (C). The other three
objects appear to start and end with approximately the same velocity.
For object (C) the velocity decreases in magnitude as the object moves
to the right. Students who answer (5) because they realize that the
average acceleration of C is negative and think zero is larger should
not be considered wrong.

Background

It is important for students to develop multiple ways of interpreting
concepts. This ensures that students are not just following rote
procedures to answer questions. Once an idea is understood students
should be able to use their understanding in a variety of contexts and
with a variety of representations.

The concept of average acceleration depends only on the initial and
final velocity over some specified time interval. Some students will
make their judgments on the basis of changes in the velocity at
different points in the motion.

Questions to Reveal Student Reasoning

How is the average acceleration determined? What is the difference
between average acceleration and instantaneous acceleration? Where is
the instantaneous acceleration greatest?

Suggestions

Draw velocity vs. time graphs for the objects (A) and (B). Analyze the
average acceleration (instantaneous acceleration) for different time
intervals (times).

A2L Item 014

Goal: Analyze and evaluate a solution to a given problem.

Source: UMPERG

A skateboarder heads straight up a steep bank angled at 45°, the whole time experiencing a constant acceleration. She manages to move 1.6m up the incline before rolling back down. The entire maneuver takes her 1.8 s, half of which is going up, the other half going down. What magnitude acceleration did she experience while on the incline?

Consider the steps in the following procedure. If the procedure is incorrect, respond with the number of the first incorrect step; if not, respond with step 7.

  1. The velocity vs. time graph for the situation is as shown.
  2. It takes the skateboarder 0.9 s to reach the highest point.
  3. The shaded area of the graph equals her displacement along the incline which is 1.6m.
  4. Equate this area (1/2 (0.9)v) to 1.6 and solve for v.
  5. Use v to find the slope of the velocity vs. time graph.
  6. The slope is equal to the acceleration.
  7. The procedure is correct.

Commentary:

Answer

(1) The graph does not describe the situation. The acceleration is constant. The velocity is not zero at t=0s, but is zero at t=.9s.

Background

This question requires students to make decisions and judgements which are needed when solving kinematics problems with understanding. This provides another opportunity to check students skills interpreting graphs and connecting the graph to the physical situation. Students may still be looking at superficial features of the graph to determine its validity.

Questions to Reveal Student Reasoning

Where is the skateboarder’s velocity zero? … velocity largest? Does this information match the graph?

What is her initial position? … her final position? Does this information match the graph?

Suggestions

Write out the appropriate solution plan. Ask students to compare the answers for the two approaches. Does an invalid plan necessarily lead to an incorrect answer? Why or why not? Does a valid plan necessarily lead to a correct answer? Why or why not?