Goal: Link acceleration to the slope of a velocity/time graph
Source: CT151.2-6
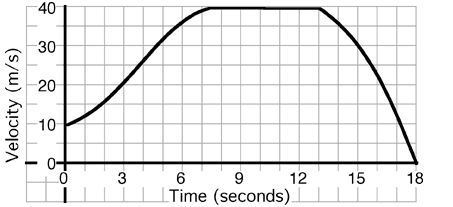
An
object’s motion is described by the graph above. The instantaneous
acceleration at t=10 sec is most nearly…
- 0 m/s2
- -2 m/s2
- 3 m/s2
- -4 m/s2
- 5 m/s2
- Other
Goal: Link acceleration to the slope of a velocity/time graph
Source: CT151.2-6

An
object’s motion is described by the graph above. The instantaneous
acceleration at t=10 sec is most nearly…
Goal: Problem solving and developing strategic knowledge
Source: UMPERG-ctqpe101
You are given this problem:
A
block sits on a frictionless incline. Given the angle of incline, the
distance along incline, and the mass of block, find the acceleration
after traveling a distance d.
What principle would you use to solve the problem MOST EFFICIENTLY?
(2) The 2nd law is needed to find the acceleration. Students who
answer that only kinematics is needed are relying on memory.
Goal: Problem solving with kinematics
Source: CT151.2-4
Ann is running with a constant speed of 3 m/s on a straight track. Deb
is also running with constant speed but is initially 10 m behind Ann. If
Deb catches up to Ann after Deb has traveled 55 m, how fast is Deb
running?
(6) The correct speed is 3.67 m/s. Students indicating #2 or #3
are likely making an arithmetic error. Have students graph the position
vs. time graphs for each runner.
Goal: Developing a strategic approach to problem solving
Source: CT151.2S02-44 spinoff
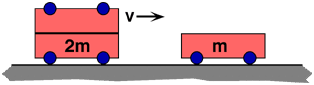
A cart
of mass 2m collides and sticks to a cart of mass m that is initially at
rest. The combination of the two then moves together. Which of the
following principles would be the most efficient way to find the final
speed of the combination?
(4) It is valuable to always associate conservation of momentum
with the third law. In addition, it is worthwhile to distinguish totally
inelastic collisions from typical inelastic collisions.
Goal: Explore momentum concepts
Source: CT151.2S02-44
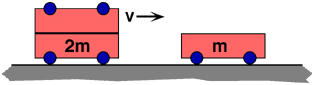
A cart
of mass 2m collides and sticks to a cart of mass m that is initially at
rest. What is the speed of the combination after the collision?
(2) This question is useful for probing pre-existing ideas about
momentum, and also for distinguishing momentum ideas from kinetic
energy. It should be used just after, or even before, covering momentum
concepts.
Usually students starting momentum already have had some energy, and
kinetic energy in particular. If appropriate, they can be asked if
energy is lost in the collision. Is more or less energy lost if the
carts do not stick together?
Goal: Hone the concept of displacement
Source: CT151.2-2
Bekki walks 3 m to the right, 4 m to the left, 5 m to the right, and 2 m
to the left. What is her displacement?
(3) Students need to distinguish between distance and
displacement. Questions such as this are good introductions to vectors.
Goal: Distinguish distance traveled from displacement
Source: CT151.2-1
Andy has the following series of displacements: 3 m to the right; 4 m to
the left; 5 m to the right; and 2 m to the left. What is his distance
traveled?
(8) Students just learning about vectors and displacements are
inclined to over specify quantities. Before they knew anything about
vectors they used distance as a scalar but can become confused and give
it the direction of the total displacement.
Goal: Hone the concept of impulse
Source: UMPERG-ctqpe80
A MOVING car collides with a STATIONARY truck. Which of the following
statements is true about the magnitudes of the impulse on each due to
the other?
(3) The 3rd law requires that the impulses be equal. Even
students who understand the 3rd law have difficulty realizing that the
magnitude of the impulse on two interacting bodies is the same. Many
students, however, do not understand impulse enough to recognize the
association. Others do not read the problem carefully enough and answer
with regard to ALL the forces, not just the one due to the other
vehicle.
Goal: Reason with kinematics
Source: UMPERG-ctqpe75
Two identical steel balls are released from rest from the same height,
and travel along tracks as shown and labeled below.

Which ball reaches the end of its track first?
(2) The ball on track B accelerates down the second slope. A
component of this acceleration is in the x-direction. This means that
the x component of ball B’s velocity is never smaller than that of ball
A. Since the tracks have the same x-dimension, ball B gets there first.
A large majority of students choose answer C incorrectly thinking that
since the balls return to the same height, they have the same speed and,
therefore, arrive at the same time.
Goal: Reason with kinematics
Source: UMPERG-ctqpe76
Two identical steel balls are released from rest from the same height,
and travel along tracks as shown and labeled below.

Which reaches the end of its track first?
(2) The ball on track B accelerates down the second slope. A component
of this acceleration is in the x-direction. This means that the x
component of ball B’s velocity is never smaller than that of ball A.
Since the tracks have the same x-dimension, ball B gets there first.
A large majority of students choose answer C incorrectly thinking that
since the balls return to the same height, they have the same speed and,
therefore, arrive at the same time.
Commentary:
Answer
(1) Useful follow-up questions include; when does the object have
positive acceleration, when negative acceleration; does the object ever
stop?; when is it farthest from the origin?