Goal: Hone the concept of work for a thermodynamic system
Source: UMPERG-ctqpe190
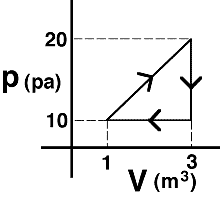
An
ideal gas is taken around the process shown. The net work done
on the gas is most nearly…
- 20 J
- -30 J
- 15 J
- -10 J
- none of the above
- cannot be determined
Goal: Hone the concept of work for a thermodynamic system
Source: UMPERG-ctqpe190

An
ideal gas is taken around the process shown. The net work done
on the gas is most nearly…
Goal: Problem solving with dynamics
Source: UMPERG-ctqpe168

A
uniform disk with mass M and radius R rolls without slipping down an
incline 30° to the horizontal. The friction force acting through
the contact point is
(4) This problem requires students to use the 2nd law written in
terms of the CM acceleration and the rotational dynamic relation written
about the CM or the contact point. In either case they also need the
geometric constraint for rolling. This is a difficult problem for
students requiring a lot of additional knowledge, such as the moment of
inertia for a disk and, depending upon solution method, the Parallel
Axis Theorem.
Having gone to the trouble of solving the problem it is best to make
sure that the students glean as much as they can. A good followup
question is which would have a larger friction force, a hoop, a disk or
a sphere. They may try to reason from the acceleration of these objects
that the larger the acceleration, the smaller the friction force. The
friction force depends upon the mass, however, and the question cannot
be answered without knowledge of the masses.
Goal: Problem solving
Source: UMPERG-ctqpe160
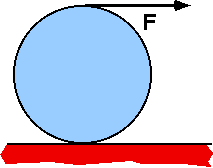
A
uniform disk with R=0.2m rolls without slipping on a horizontal surface.
String is pulled in the horizontal direction with force 15N. Moment of
inertia of disk is 0.4 kg-m2. The acceleration of the center
of the disk is most nearly
(2) This problem can be done without knowing anything about the
friction force. To do so, though, requires knowing the Parallel Axis
Theorem for moments of inertia and the constraint between the linear and
rotational rates of motion for a rolling object. An alternate method is
to write the two equations for the linear motion of the center of mass
and the torque relation for rotation about the CM and then eliminate the
friction from the two equations.
Goal: Problem solving with rotational dynamics
Source: UMPERG-ctqpe167

A
uniform disk with mass M and radius R rolls without slipping down an
incline 30° to the horizontal. The acceleration of the center of
the disk is
(5) The acceleration must be smaller than for a mass sliding on a
frictionless incline, but larger than for a hoop. Application of the
rotational dynamic relation τ = Ipαp about point P, the disk’s contact
point with the incline yields an acceleration of g/3. Students must know
the moment of inertia of the disk about its center and use the Parallel
Axis Theorem.
Good discussion questions are: Would a marble have a larger or smaller
acceleration than a coin? Would the angle of the incline matter?
Goal: Problem solve with rotational dynamics
Source: UMPERG-ctqpe156
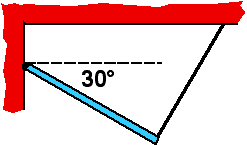
A
uniform rod is hinged to a wall and held at a 30° angle by a thin
string that is attached to the ceiling and makes a 90° angle to rod.
The tension in the string is 10N. The weight of the rod is about
(4) Some students will use the wrong trigometric function and
conclude that the weight is 40N.
An interesting follow up question is to ask what is the hinge force.
Students often forget that both the sum of the forces and the sum of the
torques must be zero for static equilibrium.
Goal: Reasoning and hone the concept of torque.
Source: UMPERG-ctqpe152
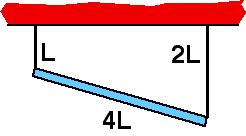
A
uniform rod of length 4L, mass M, is suspended by two thin strings,
lengths L and 2L as shown. What is net torque about the left end of the
rod?
(1) Since the rod does not rotate the total torque must be zero
about any point. Many students overworry this problem not realizing
that, independent of the angle of the rod, the other string is twice as
far as the center of mass of the rod.
Goal: Reason with impulse and energy
Source: CT151.2S02-46
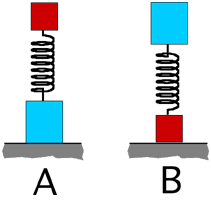
Two
blocks are connected to the ends of a spring as shown. Assume that the
mass is proportional to the size of the block. The spring is compressed
(same amount) and released suddenly. In which orientation will the
system achieve the largest height?
(2) This is a very rich problem for reasoning. It IS possible for
students to reason to the correct solution if they consider appropriate
concepts. To help them along suggest the following: Draw free body
diagrams for each of the masses separately. Combine them to get a valid
free body diagram for the system. Such a process reveals that the normal
force is responsible for the impulse causing the system to jump. The
spring force is internal to the system and does not appear on the
system’s free body diagram.
Students can deduce the answer using analogy or experience. Pogo sticks
or even the human body are analogous systems.
Goal: Problem solving with rotational dynamics
Source: UMPERG-ctqpe148
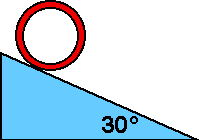
A hoop
of mass 4 kg and radius 10 cm rolls without slipping down an incline
30° to the horizontal. The acceleration of the center of the hoop
is most nearly
(4) Students should realize that the acceleration must be less
than a sliding mass on a frictionless surface would have which is #2.
Engage the students in a discussion of why the acceleration cannot
depend upon the radius.
Goal: Distinguish between mass, gravitational force and weight.
Source: CT151.2S02-21
An astronaut floats inside an orbiting spacestation. Which of the
following are true?
- No forces act on the astronaut.
- The astronaut has no mass.
- The astronaut has no
weight.
The only possible answers are #3 and #8. The issue turns on the
definition of weight. At the surface of the earth weight and the
gravitational force are often considered equivalent. Further, since the
gravitational force depends upon the mass, mass and weight are
proportional and mass units are sometimes used as a measure of weight.
In orbit bodies still experience a gravitational force but are said to
have no weight. Is it any wonder that students are confused? Invoking
scale readings as weight is not a solution either as one’s weight would
change in an elevator. The best solution to this is to sensitize
students to these issues and charge them with the responsibilty of
determining how to interpret these quantities in context.
Goal: Recognizing forces on current elements
Source: 283 Force on a half-loop
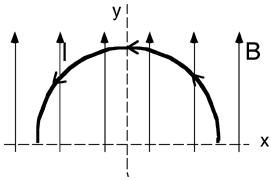
A
semicircular wire lies in a plane as shown. The positive z-direction is
out of the plane. The wire has current, I, in the counterclockwise
sense, and it is in a uniform external magnetic field, B, directed along
the +y axis. What is the direction of the net force, if any, acting on
the wire?
(6) Since the current carrying semicircle lies in the x-y plane,
as does the magnetic field, the net force, if any, must point
perpendicular to the plane, or in the z direction. For the semicircular
wire, all force contributions add. There is no contribution to the net
force from current elements near the x-axis.
The force on the missing half of the loop would be out of the page.
Together both forces on a full loop would create a torque tending to
align the field of the current loop with the external field. If
appropriate relate this situation to the torque on a magnetic dipole.
Commentary:
Answer
(4) The work done ON the system is the negative of the area of
the triangle. Students selecting answer #1 or #3 need to be sensitized
to the difference between work done on the gas versus by the gas.