Goal: Recognizing acceleration in graphs of position vs. time
Source: UMPERG
The plot of position versus time is shown for three objects. Which object has the largest acceleration at t = 2.5s?
Goal: Analyze and evaluate a solution to a given problem.
Source: UMPERG
An airplane accelerates down a runway in order to take off
but aborts and applies brakes causing the plane to stop. The plane
speeds up at a constant rate for 5 seconds, then slows down at the same
rate when the brakes are applied. The plane stops at a point that is
100 meters from its initial position. What was the acceleration of the
airplane during the first 5 seconds?
(A) The acceleration of the plane is constant and the same for the
entire motion.
(B) The entire process takes 10 seconds and the displacement is 100
meters.
(C) It is possible, therefore, to use the formula “change in x =
vo,x t + 1/2 ax t2“, where
vo,x is zero and t = 10s.
(D) The only unknown in this equation is ax, so solve for it.
Which of the following is true?
(5) More than one statement is incorrect. The
acceleration is not constant for the entire motion and so (A) is
incorrect. Although the magnitude of the acceleration is constant its
direction changes. Statement (C) is incorrect because the formula in
(C) is only valid over periods the acceleration is constant.
This question requires students to make decisions and judgements which
are needed when solving kinematics problems with understanding. The
kinematics equations are of limited use. They apply directly only to
problems involving constant acceleration. Students are usually not
aware of this limitation and are apt to apply the kinematics expressions
much too broadly. Students also tend to view acceleration as a scalar
quantity and therefore see the acceleration as constant even when it is
not so.
How do we determine the acceleration. What is the acceleration while
the plane is speeding up? … slowing down? If necessary ask the
following. What is the direction of acceleration while the plane is
speeding up? … slowing down?
Draw a graph of velocity vs. time for constant acceleration. Draw a
graph of velocity vs. time for the problem situation. Discuss the
acceleration and displacement in terms of these graphs.
Goal: Relate friction, velocity, and time.
Source: UMPERG
A cart rolls across a table two meters in length. Half of the length of
the table is covered with felt which slows the cart at a constant rate.
Where should the felt be placed so that the cart crosses the table in
the least amount of time?
The
felt should be placed on the second half of the table. After the cart
rolls across the felt it will travel at a lower speed. To minimize the
time to cross the table one must minimize the time the cart spends at
the lower speed. The graph to the right illustrates the point for the
two extreme cases: felt on first half (gray curve) and felt on second
half (black curve). The velocity vs. time graph for the case where the
felt is on the second half of the table is above the velocity vs. time
graph for all other possibilities. Answer (3) is the best choice.
Students should have some experience using the concepts of velocity and
acceleration to solve kinematics problems and analyze graphs. The
question students need to answer is what configuration will permit the
cart to travel at a higher speed for the longest period of time (or the
lowest speed for the shortest period of time). A graph provides support
for a conceptual argument.
Issues to consider: (1) Can students reason and analyze a situation
involving constant acceleration. (2) Do students try to solve the
problem using algebraic methods? (2) Can students use graphical methods
and conceptual reasoning? (3) Can students verbalize the central idea —
an object will travel a certain distance in less time if its speed is
higher?
Where is the cart moving the fastest? … the slowest?
What does a graph of the velocity vs. time look like?
How do you determine when the cart has reached the end of the table from
a graph of velocity vs. time?
Try some limiting cases. If the piece of felt were small (say 10 cm)
but slowed the cart from 1 to .8 m/s on a 3m table. Approximately how
long would the trip take if the felt were placed at the beginning of the
table?…at the end of the table?
Goal: Relate acceleration to slope of velocity graph
Source: UMPERG
A toy rocket blasts off with an acceleration of 9.8 m/s2
upward. After 5 seconds the rocket releases its “payload” but continues
to accelerate upward at the same rate. In the following graph the solid
line represents the velocity of the rocket as a function of time and the
dashed line represents the velocity of the payload.
Which of the following statements regarding this situation are correct?
A. The payload hits the ground at t = 10s.
B. The slope of the rocket’s velocity vs. time graph is 9.8 m/s2.
C. The velocities of the rocket and the payload point in opposite
directions after the payload is released.D. The area of the shaded region can be determined from the given
information.E. The payload spends half the time in the air as the rocket.
F. The payload is released at 1/2 the maximum height of the rocket.
Answer (7) is the best choice. The only statements that are true are
(B) and (D). The height of the rocket in relation to the height of the
payload can be determined by the ratio of the areas under their
respective velocity vs. time graphs. The payload reaches its maximum
height at t=10s (i.e., when its velocity is equal to zero). At t=10s the
area under the rocket’s v vs. t graph is twice the area under payload’s
v vs. t graph. This can be determined without knowing any of the
information contained in (A) through (F).
Issues to consider: (1) Can students identify and evaluate information
needed to judge the correctness of a statement? (2) Can students
interpret a graphical representation of information? (3) Can students
determine the point of maximum displacement from a v vs. t graph? (4)
Can students interpret the significance of slope and area for a v vs. t
graph. (5) Do students confuse v vs. t graphs with x vs. t graphs.
When does the payload start to fall back toward the earth? When does
the payload hit the earth? What is the acceleration of the payload
after it is released?
Which of the statements are true? Explain. Which of the statements are
false? Explain.
Could the true statements be used to determine the heights of the rocket
and payload? Explain.
As a class draw a rough strobe diagram. Relate times in the strobe
diagram to times on the graph.
Discuss with students how they would approach the problem algebraically.
Goal: Linking acceleration to changes in velocity.
Source: UMPERG
A marble rolls onto a piece of felt that is 30 cm in length. At 20 cm
the speed of the marble is half of its initial value. Which of the
following is true? Assume that the acceleration is constant on the felt.
(1) The marble will come to rest on the felt. A graph of velocity vs. time is helpful for analyzing this problem. The distance traveled while slowing down to half its initial speed (i.e., the first 20 cm) is three times the additional distance (i.e., the distance beyond 20 cm) the marble will roll before coming to rest. This can be seen by comparing the areas for
these two different time periods. The marble will come to rest at approximately 26.7 cm.
Students should have some experience using the concept of acceleration to solve kinematics problems and analyze graphs. The answer is less important than how students represent the problem and how they approach solving the problem.
Issues to consider:
(1) Do students only solve the problem using algebraic methods? (2) To what extent do students use other approaches? (3) Do students use graphical methods involving areas? (4) Do theycompare average speeds for the two periods (i.e., the period covering the first 20 cm and the remaining period of time before the marble comes to rest)? (5) Do they compare the actual speeds of the marble at each instant of time for the two time periods (the ratio is usually greater than or equal to 2/1 at each corresponding time, as shown in the accompanying graph). (6) Even if the students use algebraic methods, do they employ a strategy or do they do so mindlessly?
Ask students to consider the following context (which they are familiar with and is algebraically simple): an object is dropped from rest. How fast is it moving after one second? … after two seconds? …after three seconds? How far has it traveled after one second? …after two seconds?…after three seconds? What is the relationship between velocity and position? Why is the relationship not linear?
If students do not use a graph to solve the problem, ask them to draw a velocity vs. time graph for the situation and then use the graph to solve the problem.
A demonstration is possible.
Goal: Contrast instantaneous and average acceleration. Explore the difference between them.
Source: UMPERG
Which of the following motions has a zero value for the average
acceleration during the specified time interval?
A. A race car makes one lap around an oval track at constant speed.
The time interval is the time to complete the lap.B. A cart collides with a wall and rebounds with the same speed. The
time interval is the time during which the cart is in contact with the
wall.C. A ball rolls up, then down a hill. The time interval is the time
the ball is on the hill.
Situation A is the only one where the velocity is the
same at the beginning and end of the time interval. Therefore, it is
the only situation where the change in velocity is zero. Answer (1) is
the best choice.
Use this item early in the
study of acceleration. It requires that students be familiar with the
definition of average acceleration. Issues: (1) Do students have a
working knowledge of the vector nature of velocity and acceleration?
(2) Do students incorrectly think that the average acceleration must be
zero if an object’s speed is the same at the beginning and end of the
time interval, even if the direction of the velocity vector at these two
times is different. (3) Do students correctly perceive that the
velocity is different when an object changes direction?
What is the definition of average
acceleration? How do you compute the average acceleration for a given
time interval?
How can you tell if the velocity has changed? If an object has the same
speed at two different times, is the average acceleration necessarily
zero? Why, or why not?
What are some good rules of thumb for ascertaining whether or not the
average acceleration of an object is zero for a given time interval?
Have students write out examples of motion
for a finite time interval. Have students present their examples to the
class. Have the class decide whether the average acceleration is zero.
Let the class devise ways of determining whether the average
acceleration in a certain situation is zero.
Goal: Honing the idea of constant acceleartion.
Source: UMPERG
A baseball is shot into the air from a spring loaded cannon. The diagram shows the ball at five locations. At which location is the magnitude of the acceleration least?
The ball’s acceleration is 9.8 m/s2 (down) throughout its
entire motion (assuming air resistance can be neglected). Answer (8) is
the best choice.
Students should have some experience analyzing the velocity of objects
undergoing free-fall motion. Issues to consider: (1) Do students think
that the acceleration is zero at the maximum height, where the ball
momentarily stops? (2) Do students think that the acceleration points
in the same direction as the velocity? (3) Can students apply the
definition of acceleration to a familiar situation?
The goal is to have students confront existing misconceptions: 1)
Students often believe that the acceleration must point in the direction
of the motion; and 2) Students often believe that the acceleration is
9.8 throughout free fall but zero at the top of the trajectory since the
vertical speed is zero there.
Ask students to apply the operational definition of acceleration (take
the velocity vector just after C and subtract the velocity vector just
before C and divide by the time interval). Have them compare the x/y
component of the velocity just before C with the x/y component of the
velocity just after point C.
For students who persist in thinking that both the velocity and
acceleration are zero at the top of a trajectory, contrast the
subsequent motion with that of an object sitting at rest on a surface.
Goal: Differentiate velocity and acceleration in the context of free-fall motion.
Source:
A person throws a ball straight up in the air. The ball rises to a maximum height and then falls back down so that the person catches it. Consider the ball while it is in the air.
Which of the following statements are true?
A. Just after the ball leaves the person’s hand the direction of the acceleration is up.
B. The acceleration is zero when the ball reaches its maximum height.
C. The acceleration is about 9.8 m/s2 (down) when the ball is falling.
After the ball leaves the person’s hand, its acceleration is 9.8 m/s2 (down) throughout the entire motion (assuming air resistance can be neglected). Answer (3) is the best choice.
Use this item during kinematics, shortly after the introduction of “acceleration.” We suggest that students have some experience analyzing the velocity of objects undergoing freefall motion. Intended focus: (1) Do students think that the acceleration is zero at the maximum height, where the ball momentarily stops? (2) Do students think that the acceleration points in the same direction as the velocity? (3) Can students apply the definition of acceleration to a familiar situation?
The goal is to have students confront existing misconceptions:1) Students often believe that the acceleration must point in the direction of the motion; and 2) Students often believe that the acceleration is 9.8 throughtout free fall but zero at the top of the trajectory since the vertical speed is zero there.
Have students sketch the velocity of the ball as a function of time. Ask how the acceleration is related to this graph.
Using Microcomputer Based Lab software and a sonic ranger, generate a velocity graph for a cart going up and down an incline. Discuss how the graph relates to a velocity vs. time graph for a ball thrown vertically.
Goal: Hone the concept of acceleration.
Source: UMPERG
HOW MANY of the identified objects are NOT accelerating?
Enter the number of objects, or 8 for “none” and 9 for “cannot be determined”.
Only the skydiver, who has reached terminal velocity, has zero acceleration. In each of the other situations, the acceleration is nonzero because either the speed or the direction of motion is changing. Answer (2) is the best choice.
Context for Use: Give after introducing the concept of acceleration. Intended focus: What factors/criteria do students use to determine whether an object is accelerating? The goal is to focus students on changes in the speed/direction of an object’s motion.
How do you know whether an object is accelerating? What are some examples of objects undergoing acceleration? If an object is falling is it necessarily accelerating?
In some cases did you need to make assumptions before deciding whether the object was accelerating? (Ask students to provide examples.)
Have students write out how they determine whether an object is accelerating. After discussing the different methods, have students vote on which one they think is best.
Play a “challenge game” with the class. Two teams of students think of situations in which an object undergoes some motion. The teams then take turns challenging each other to determine whether or not the objects are accelerating.
Goal: Interrelate representations of acceleration and identifying potential misconceptions.
Source: UMPERG
Which of the following statements are true?
A. While an object moves at constant speed, its acceleration must be zero.
B. For a ball to roll up a hill and then back down, its acceleration must change.
C. When an object’s velocity versus time graph crosses the time axis, its acceleration must be zero.
Answer (8) is the best choice. An object’s acceleration is nonzero if its direction of motion is changing, or its speed is changing, or both. A constant speed does not imply zero acceleration because the object’s direction of motion could be changing. Therefore (A) is false. An object will have a nonzero acceleration if its velocity is changing, even if its velocity is (instantaneously) zero. Therefore (C) is false. For a ball that rolls up a hill and then back down, the acceleration can be constant. This will be the case if the hill has a constant slope, and the friction and air resistance forces are small. Therefore (B) is also false.
Assessment Issues: (1) Do students know that an object has a nonzero acceleration whenever its speed or direction of motion change? Do they think that the speed must change for there to be a nonzero acceleration? (2) Do students confuse velocity and acceleration? Do they think that the acceleration is positive/zero/negative whenever the velocity is positive/zero/negative? (3) Do students use graphs and pictures to answer this question?
Have one group of students perform some motion (perhaps by walking or moving an object), and challenge another group to graph position versus time, velocity versus time, or acceleration versus time for that motion. (If the motion performed is in two dimensions, students should graph one of the components of the motion.)
Commentary:
Answer
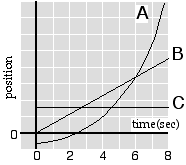
(1); the slope of position v. time is velocity, and the slope of
velocity v. time is acceleration. The only plot with a non-zero
(positive) acceleration is A. Plot C denotes zero velocity, and plot B
denotes a constant velocity.
Background
It is important for students to develop multiple ways of interpreting
concepts. Graphical representations are often more useful than
algebraic representations in solving kinematic problems. In this
instance students must recognize the signature of acceleration in a plot
of position vs time.
Questions to Reveal Student Thinking
How can you determine if an object is accelerating? For which objects
is the velocity changing. What are some examples of objects moving
according to the graphs?
What features about a position vs. time graph indicate that an object
has a zero velocity? a zero acceleration? What features indicate a
negative acceleration? a positive acceleration?
Suggestions
Draw a graph of velocity vs. time for each object. Then draw the graph
of acceleration vs. time.
Follow up question: Can the position vs. time of an object have a
negative slope at some specific time, and yet the acceleration be
positive at that same time?