Goal: Link acceleration to the slope of a velocity/time graph
Source: CT151.2-6
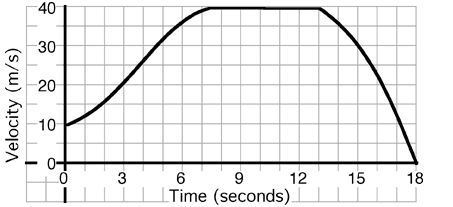
An
object’s motion is described by the graph above. The instantaneous
acceleration at t=10 sec is most nearly…
- 0 m/s2
- -2 m/s2
- 3 m/s2
- -4 m/s2
- 5 m/s2
- Other
Goal: Link acceleration to the slope of a velocity/time graph
Source: CT151.2-6

An
object’s motion is described by the graph above. The instantaneous
acceleration at t=10 sec is most nearly…
Goal: Interpreting graphs
Source: CT151.2-5
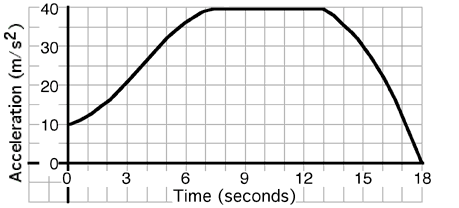
An
object’s motion is described by the graph above. The average
acceleration during the first 10 s is most nearly…
(3) Students may have difficulty understanding what they are
asked. Recasting the problem in terms of areas helps. The only
contenders should be #2 or #3. Counting blocks should make it clear that
the result is much closer to #3.
Goal: Hone reading graphical depictions of thermodynamic cycles.
Source: UMPERG-ctqpe216
A quantity of ideal gas undergoes a thermodynamic process. Which curve
represents an isobaric path?
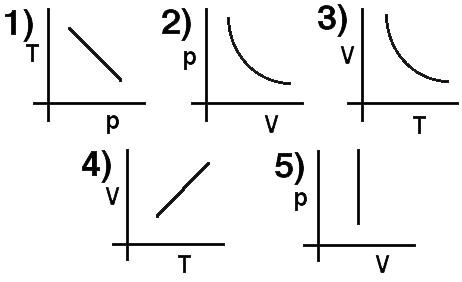
(4) If V is linearly related to T the perfect gas law implies that the
pressure is constant.
Goal: Hone the concept of work on a gas
Source: UMPERG-ctqpe220
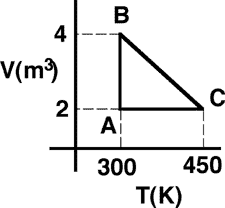
One mole of an ideal monatomic gas is taken around the cycle shown.
The work done on the system during the process B to C is
(1) Positive work is done ON the system. Since the path on a V-T diagram
is a straight line, the process is isobaric.
Goal: linking acceleration and velocity graphically.
Source: UMPERG
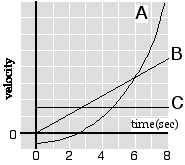
The
plot of velocity versus time is shown at right for three objects. Which
object has the largest acceleration at t = 2.5s?
(6) Objects (A) and (B) have the same acceleration (i.e., they have the
same slope for the velocity vs. time graph at t=2.5s) Object (C) has a
constant velocity (zero slope).
After students have been introduced to acceleration, but before they are
given a procedure for determining the acceleration from a graph of
velocity vs. time. Students should answer this question after they have
gained an understanding of the definition of acceleration, but before
they are given any explicit instruction for how acceleration relates to
a velocity vs. time graph.
How can you determine if an object is accelerating? For which objects
is the velocity changing. What are some examples of objects moving
according to the graphs?
What features about a velocity vs. time graph indicate that an object
has a zero velocity? Zero acceleration? What features indicate a
negative acceleration? Positive acceleration?
Redraw the velocity vs. time graph for object (A) twice more. In one
drawing approximate the curve with three straight line segments. In the
second approximate the curve with 6 straight line segments.
Goal: Associate velocity graph with physical motion.
Source: UMPERG
A soccer ball rolls across the road and down a hill as shown below.
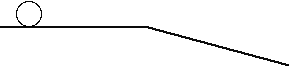
Which of the following sketches of vx vs. t represents the
horizontal velocity of the ball as a function of time?
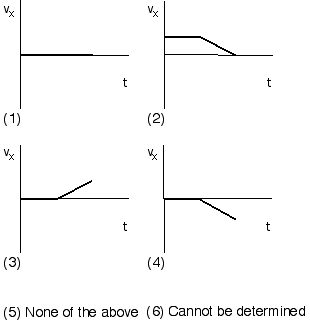

(5) None of the above. The ball crosses the road in a straight line at
a more-or-less constant speed (perhaps slowing down slightly) provided
that the road is in good condition and the rolling friction between the
ball and road is sufficiently small. As the ball rolls down the hill it
will speed up, and so there will be an acceleration in the direction of
motion, with a non zero component to the right. The following graph is
a reasonable representation of the horizontal velocity as a function of
time.
This problem could challenge students in several areas: (1) Can
students recognize how the velocity is changing? What criteria do they
use? (2) Do students realize that as the ball moves down the hill it
speeds up and the x-component of velocity increases? Students may
associate the increase in velocity with the y-direction only. (3) Do
students associate the graph with the terrain over which an object
travels? The process of translation of a motion quantity to a graph can
be very difficult for students. (4) Will students confuse motion
quantities? When students analyze the graphs of velocity vs. time they
may be interpreting the graphs in terms of position instead of velocity.
Is the velocity ever zero? Where does the ball speed up? …slow down?
What is the direction of the velocity while the ball is on the sloped
section? Does the velocity have a non-zero horizontal component?
Set up a demonstration with a horizontal surface and a ramp, both with
the same net horizontal displacement. Roll a ball slowly across the
horizontal surface and down the ramp. Ask students to judge which
horizontal displacement took more time. Over what section (horizontal
surface or ramp) is the velocity larger on average?
Goal: Recognize forces and the correct free body diagram.
Source: UMPERG
A car accelerates down a straight highway. Which of the free-body
diagrams shown below best represents this situation?
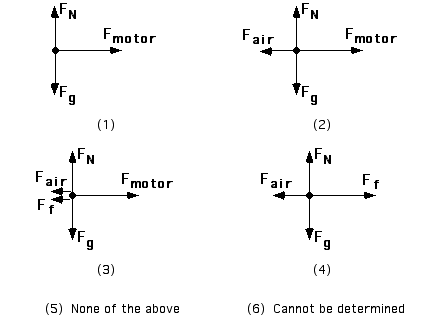
(4) is the best response. Students often think of the motor as the source of force propelling the car when it is the friction force on the tires that enable the car to move forward. Sometimes it helps to discuss the process of walking on a perfectly slippery surface (ice) to enable students to see the role of friction for forward motion.
Goal: Reasoning and comparing the sizes of forces.
Source: UMPERGA block attached to the end of a spring is hanging at rest from the
A block attached to the end of a spring is hanging at rest from the
ceiling as shown at the left below. After the block is pulled down and
released it moves up and down for an extended period of time. The
motion during one cycle is shown in the graph at right below.
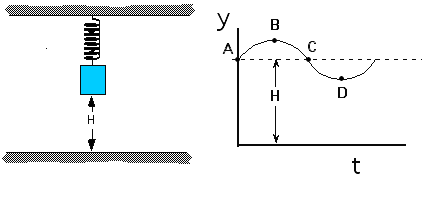
Several points are indicated on the graph. At which point is the spring
force exerted on the block the greatest?
(4). The spring force is largest at the position where it is compressed
or stretched the most relative to its natural length. The spring is
already stretched when it is at a height H because there must be an
upward spring force to balance the gravitational force on the block. As
the height of the block is decreased the spring is stretched further.
As the height of the block is increased the spring is stretched less –
if raised enough the spring would start to compress.
Many students will attempt to apply the spring force law without real
understanding. This problem requires students to understand the
physical situation and to interpret graphical information about the
height of the block to reason out an answer.
What is the force law for a spring? How does the spring force compare
to the weight of the block? At what points is the spring stretched? …
compressed?
Demonstrate with a spring that a vertical spring stretches when a weight
is attached. Show that as the weight moves up and down that the spring
need never get back to its natural length (i.e., it is always stretched)
Draw free-body diagrams, especially for points B and D.
Goal: Translate a verbal description of physical motion to graph of force.
Source: UMPERG
A block is dropped onto a vertical spring. Which net force vs. time
graph best represents the net force on the block as a function of time?
Consider only the motion of the block from the time it is dropped until
it first comes to rest.
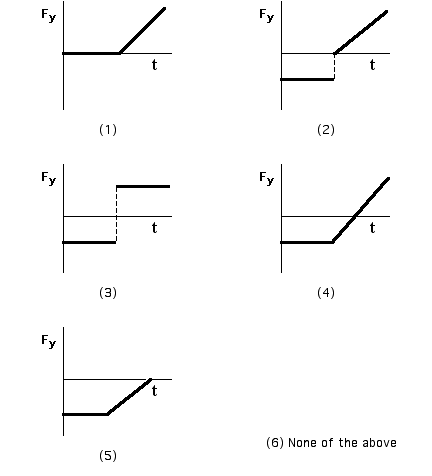
(4); Some students may select (5) confusing the equilibrium point with the point where the block comes to rest. Students selecting (2) are ignoring gravity after the block hits the spring.
Goal: Translate between representations of motion
Source: UMPERG
The strobe diagram below shows the position of an object at successive
equal time intervals. The object moves from left to right.
Consider the following situations:
A. A book slides down an incline, moving from a rough region onto a
smooth region.
B. A cart is connected to a compressed spring and released.
C. A ball is dropped, hits the ground and rebounds to its initial
position.
D. A runner runs a race.
Which of these situations could be roughly described by the strobe
diagram?
(2),(4) or (7); Depending upon assumptions (B) or (D) are possible. The cart leaving the spring would speed up then eventually slow down due to friction. Also, the runner will speed up and eventually slow down.
Commentary:
Answer
(1) Useful follow-up questions include; when does the object have
positive acceleration, when negative acceleration; does the object ever
stop?; when is it farthest from the origin?