Tag Archives: Graphing

A2L Item 008

Goal: Relate acceleration to slope of velocity graph

Source: UMPERG

A toy rocket blasts off with an acceleration of 9.8 m/s2
upward. After 5 seconds the rocket releases its “payload” but continues
to accelerate upward at the same rate. In the following graph the solid
line represents the velocity of the rocket as a function of time and the
dashed line represents the velocity of the payload.

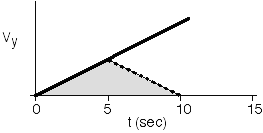
Which of the following statements regarding this situation are correct?

A. The payload hits the ground at t = 10s.

B. The slope of the rocket’s velocity vs. time graph is 9.8 m/s2.

C. The velocities of the rocket and the payload point in opposite
directions after the payload is released.

D. The area of the shaded region can be determined from the given
information.

E. The payload spends half the time in the air as the rocket.

F. The payload is released at 1/2 the maximum height of the rocket.

  1. Only (A)
  2. Only (B)
  3. Only (C)
  4. Only (D)
  5. Only (E)
  6. Only (F)
  7. Two of the statements are true
  8. Three of the statements are true
  9. None is true

Commentary:

Answer

Answer (7) is the best choice. The only statements that are true are
(B) and (D). The height of the rocket in relation to the height of the
payload can be determined by the ratio of the areas under their
respective velocity vs. time graphs. The payload reaches its maximum
height at t=10s (i.e., when its velocity is equal to zero). At t=10s the
area under the rocket’s v vs. t graph is twice the area under payload’s
v vs. t graph. This can be determined without knowing any of the
information contained in (A) through (F).

Background

Issues to consider: (1) Can students identify and evaluate information
needed to judge the correctness of a statement? (2) Can students
interpret a graphical representation of information? (3) Can students
determine the point of maximum displacement from a v vs. t graph? (4)
Can students interpret the significance of slope and area for a v vs. t
graph. (5) Do students confuse v vs. t graphs with x vs. t graphs.

Questions to Reveal Student Thinking

When does the payload start to fall back toward the earth? When does
the payload hit the earth? What is the acceleration of the payload
after it is released?

Which of the statements are true? Explain. Which of the statements are
false? Explain.

Could the true statements be used to determine the heights of the rocket
and payload? Explain.

Suggestions

As a class draw a rough strobe diagram. Relate times in the strobe
diagram to times on the graph.

Discuss with students how they would approach the problem algebraically.

A2L Item 002

Goal: Interrelate representations of acceleration and identifying potential misconceptions.

Source: UMPERG

Which of the following statements are true?

A. While an object moves at constant speed, its acceleration must be zero.

B. For a ball to roll up a hill and then back down, its acceleration must change.

C. When an object’s velocity versus time graph crosses the time axis, its acceleration must be zero.

  1. Only (A)
  2. Only (B)
  3. Only (C)
  4. Both (A) and (B)
  5. Both (A) and (C)
  6. Both (B) and (C)
  7. All three are true
  8. None is true
  9. Cannot be determined

Commentary:

Answer

Answer (8) is the best choice. An object’s acceleration is nonzero if its direction of motion is changing, or its speed is changing, or both. A constant speed does not imply zero acceleration because the object’s direction of motion could be changing. Therefore (A) is false. An object will have a nonzero acceleration if its velocity is changing, even if its velocity is (instantaneously) zero. Therefore (C) is false. For a ball that rolls up a hill and then back down, the acceleration can be constant. This will be the case if the hill has a constant slope, and the friction and air resistance forces are small. Therefore (B) is also false.

Background

Assessment Issues: (1) Do students know that an object has a nonzero acceleration whenever its speed or direction of motion change? Do they think that the speed must change for there to be a nonzero acceleration? (2) Do students confuse velocity and acceleration? Do they think that the acceleration is positive/zero/negative whenever the velocity is positive/zero/negative? (3) Do students use graphs and pictures to answer this question?

Questions to Reveal Student Reasoning

  • What is the definition of acceleration? How do you determine whether an object is accelerating? For which situations is an object accelerating? (Have the students explain.)
  • What is the definition of velocity? How do you determine whether an object’s velocity is changing?
  • For which situations is the velocity changing? (Have the students explain.)
  • When is the acceleration zero in an acceleration versus time graph? … in a velocity versus time graph? … in a position versus time graph?

Suggestions

Have one group of students perform some motion (perhaps by walking or moving an object), and challenge another group to graph position versus time, velocity versus time, or acceleration versus time for that motion. (If the motion performed is in two dimensions, students should graph one of the components of the motion.)

A2L Item 001

Goal: Relating physical understanding of an object’s motion to a graphical representation of acceleration.

Source: UMPERG

A soccer ball rolls slowly across the road and down a hill as shown below:

Which of the following sketches of ax vs. t is a reasonable representation of the horizontal acceleration of the ball as a function of time?

Commentary:

Answer

We will assume that rolling friction between the ball and road surface is small and that air resistance can be ignored. We will also assume that the ball does not leave the road surface at the top of the hill. If these assumptions are satisfied, the ball will roll across the level road at a (nearly) constant velocity. As it rolls down the hill, the ball will speed up, producing a constant acceleration in the direction of motion. There will be a nonzero component of acceleration pointing to the right. The graph at the right is a reasonable representation of the horizontal acceleration as a function of time. For our assumptions, answer (5) is the best choice.

Background

Context for Use: Give after students explore the vector nature of acceleration. Formal (quantitative) kinematics is not required.

Assessment Issues: (1) Can students recognize when an object is accelerating? What criteria do they use? (2) Do students perceive nonzero horizontal and vertical components of acceleration? Do some students think that the acceleration is in the y-direction only? (3) Do students think that the acceleration graph looks like the sketch of the road on which the ball rolls? What process do they use to construct a graph of acceleration versus time? (4) Do students confuse the different motion quantities? For example, do they interpret the graphs of acceleration versus time as velocity versus time graphs?

Questions to Reveal Student Reasoning

  • Where does the ball speed up? Where does it slow down? Why does its speed change?

  • What is the direction of the ball’s acceleration while it is on the hill? Does the ball accelerate to the right? Does the ball accelerate vertically?

Suggestions

Help students construct the horizontal (and vertical) velocity vs. time graph for the ball. If students have been exposed to forces, draw a free-body diagram and use it to find the net force.