Goal: Problem solving using momentum conservation.
Source: UMPERG-ctqpe90
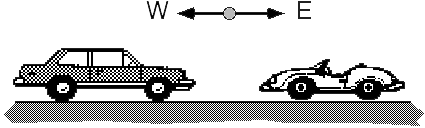
On an icy road, an automobile traveling east with speed 50 mph collides
head-on with a sports car of half the mass traveling west with speed 60
mph. If the vehicles remain locked together, the final speed is:
Goal: Hone the vector nature of impulse and contrast impulse to kinetic energy.
Source: UMPERG-ctqpe82
A block having mass M travels along a horizontal frictionless surface
with speed vx. What impulse must be delivered to the mass
to reverse its direction?
(1) or (2) or (6) are all defensible answers depending upon how students
interpret the question. This is a good question for stressing to
students that it is their reasoning not their answer that is important.
Impulse is a vector. Using the impulse-momentum relation, the change in
momentum must be at least mvx in the direction opposite to
the motion to reverse direction.
What impulse would be needed to make the mass travel parallel to the
y-axis?
Suppose a constant force Fx acts for 4 seconds causing the
mass to stop. What force would be needed to stop the mass in 2 seconds.
Have students make a concept map showing the relationships among the
quantities mass, velocity, momentum, impulse, time, force, and average
force.
Does it bother students that, in 10 seconds gravitation provides an
impulse of 10mg to a book whether it is dropped or sitting on a table?
Goal: Hone the scalar nature of work and distinguish work from impulse.
Source: UMPERG-ctqpe74
A block having mass M travels along a horizontal frictionless surface
with speed v. What is the LEAST amount of work that must be done on
the mass to reverse its direction?
(3) Zero work must be done. Students will likely become entangled in
the sign of the work as well as the interpretation of the requirement to
“reverse its direction”. The most defensible answer after (3) is (2).
Some students may confuse the sign of the work, Students who choose (2)
or (4) have career potential as a lawyer.
This is an excellent problem for engaging students in a discussion of
work and energy. A mass traveling in the opposite direction with the
same speed would have the same kinetic energy. The work-kinetic energy
theorem then states that no net work need be done on the mass. The
work-kinetic energy theorem also resolves any ambiguity in the sign of
the work if the mass is just brought to rest.
Draw a diagram indicating the direction of motion and the direction of
the force acting on the mass. What is the direction of the
displacement?
If the surface had friction and the mass just slid until it stopped, how
much work would the friction force do?
It is easy to demonstrate several situations for which an object
reverses its direction and no new work is done. All it requires is a
conservative force. For example, let a ball roll up an incline and then
back down. Or, allow a mass to encounter a spring. Or, have a marble
roll around a semicircular track. This latter case is interesting
because the force acting on the mass (Normal) does no work.
Goal: Recognize forces that do work, that is those with associated displacement.
Source: UMPERG-ctqpe52
A block having mass m moves along an incline having friction as shown in
the diagram above. The spring is extended from its relaxed length. As
the block moves a small distance up the incline, how many forces do work
on the block?
(4) Four forces do work on the block: gravitation, rope, spring, kinetic
friction (because you are told the block moves). The normal force does
no work.
Recognizing those forces that do work is an important skill for students
to master. They also need to recognize whether the work is positive or
negative.
As the block moves up the plane, which forces do positive work? negative
work? How are you determining which it is? How would your answer to the
above question change if the spring were compressed rather than
extended.
Set up some situations with blocks, springs and ropes and let students
practice identifying all the forces doing work. This is a good activity
to do in conjunction with drawing free body diagrams.
Goal: Recognizing the presence of forces.
Source: UMPERG
A block having mass m moves along an incline having friction as shown in
the diagram above. As the block moves a small distance along the
incline, how many forces act on the block?
(5) Five forces act on the block: gravitation, rope, spring, kinetic
friction (because you are told the block moves), and normal due to the
incline. Many student errors are due to the failure to identify all of
the forces acting on a body.
It is helpful to classify forces into action-at-a-distance forces, such
as gravity and electromagnetism, and contact forces. Students can then
employ a strategy for identifying all the forces since every object
touching a body will give rise to a force. The only exceptions are the
fundamental forces, which is an easily exhausted list.
Does it matter if the block is moving up the plane or down? If the block
is at rest, how many forces MUST be acting on the block? How many forces
may be acting but you can’t be sure?
Set up some situations with blocks, springs and ropes and let students
practice identifying all the forces. This is a good activity to do in
conjunction with drawing free body diagrams.
Goal: Problem solving.
Source: UMPERG-ctqpe146
A
child having mass 32kg is standing at the rim of a rotating disk of
radius 1.5m. The disk is free to rotate without friction. The disk has
moment of inertia I = 125kg-m2 and is initially at rest. The
child throws a rock of mass 4kg in the forward tangential direction as
shown in the figure with a speed of 5m/s. The final angular speed of
the disk is most nearly
(7) is the most appropriate response. Initially there is no angular
momentum in the system. The child and disk must rotate clockwise to
balance the angular momentum of the rock. Some students may forget to
add the moment of inertia of child to that of the disk.
Throwing the rock tangentially gives the rock angular momentum relative
to the fixed center of the disk. The disk-child system must have an
angular momentum which is the negative of that of the rock. Thus, it is
possible to find the angular velocity. The angular velocity is
negative, i,e, into the page.
Does the total system have angular momentum just before the rock is
thrown? just after it is thrown?
Does the rock have angular momentum just before it is thrown? just
after it is thrown?
What happens to the child upon throwing the rock? Does the child move?
How?
Have students relate their answer to this question to items 67 and 68.
Goal: Problem solving and developing strategic knowledge.
Source: UMPERG-ctqpe145
You are given this problem:
A
child is standing at the rim of a rotating disk holding a rock. The
disk rotates without friction. The rock is thrown in the RADIAL
direction [path (5)] at the instant shown. You are given:
- Mass of the child
- Radius of the disk
- Mass of the thrown rock
- Velocity of the rock
- Initial angular speed of the system
You want to find the final angular speed of the disk and child.
What principle would you use to solve the problem MOST EFFICIENTLY?
(5) is the correct response if the rock is thrown radially. Since there
is no angular impulse, there can be no change in angular momentum.
Neither the rock alone, nor the child/disk system changes angular
momentum.
Throwing the rock radially, clearly increases the kinetic energy but not
the angular momentum. Consequently, the final angular speed of the disk
and child is the same as the initial speed.
Does the rock have angular momentum (or energy) just before it is
thrown? just after it is thrown?
If energy (angular momentum) is gained, where does it come from?
Changes in angular momentum are caused by a net torque. What torques
act on the system during the process of throwing?
Have students relate their answer to this question to item 67.
Goal: Recognize physical conditions under which conservation principles hold.
Source: UMPERG-ctqpe144
A
child is standing at the rim of a rotating disk holding a rock. The
disk rotates without friction. The rock is thrown in the RADIAL
direction at the instant shown. What quantities are conserved during
this process?
(1) is the correct response if the rock is thrown radially. The change
in velocity of the rock and, therefore its change in momentum, is in the
radial direction. The net torque on the system is zero so the angular
momentum cannot change. Some students may be tempted to choose (3) but,
since the rock is thrown via biological processes (as opposed to
mechanical processes), mechanical energy is not conserved.
Throwing the rock radially, clearly increases the kinetic energy but not
the angular momentum. This item provides a mechanism for a rich
discussion of the source of the kinetic energy.
Does the rock have angular momentum (or energy) just before it is
thrown? just after it is thrown?
If energy (angular momentum) is gained, where does it come from?
Changes in angular momentum are caused by a net torque. What torques
act on the system during the process of throwing?
Have the students do a ‘thought’ experiment by considering a spring
loaded gun mounted on a rotating turntable aimed outward along a radius.
The spring is released firing a small ball outward. This situation
makes it easier for some students to identify the source of additional
kinetic energy. Further, since the force applied is parallel to the
radius, there is no angular impulse and no change in angular momentum in
the system. Have students relate their answer to this question to the
previous one. Also contrast this and the previous one to items 64 and
65.
Goal: Hone the vector nature of velocity.
Source: UMPERG-ctqpe142
A
child is standing at the rim of a rotating disk holding a rock. The
disk rotates without friction. The rock is thrown in the RADIAL
direction at the instant shown, which of the indicated paths most nearly
represents the path of the rock as seen from above the disk?
(4) is the correct path if the rock is thrown radially.
Once thrown the components of the velocity of the rock lying in a
horizontal plane are constant so the rock will have a path which is a
straight line.
Identify a coordinate frame. What are the components of the velocity
vector immediately after the rock is thrown?
What is the radial component of the velocity if the rock follows path
(2)?
Is it possible to throw the rock in such a way that the rock follows
path (5)?
This item should be compared to 63.
Goal: Recognize physical conditions under which conservation principles hold.
Source: UMPERG-ctqpe134
A
child is standing at the rim of a rotating disk holding a rock. The
disk rotates without friction. The rock is dropped at the instant
shown. What quantities are conserved during this process.
(3) is the correct response if the rock is simply dropped. Some
students may fail to include the rock as part of the system after it is
dropped.
Objects traveling in a straight line do have angular momentum with
respect to any origin that is not on the path of the object. The rock
does not cease to have angular momentum with respect to the center of
the disk when it is dropped. Although the angular momentum and energy of
the rock will change as the rock falls, its angular momentum and energy
just after it is dropped are the same as just before.
Does the rock have angular momentum (or energy) just before it is
dropped? just after it is dropped?
If energy (angular momentum) is lost, what happens to it?
Changes in angular momentum are caused by a net torque. What torques
act on the system?
Have students relate their answer to this question to the previous one.
Commentary:
Answer
(8) None of the above. This is a straightforward totally inelastic
collision situation.
Background
Students are frequently bothered by the idea of a totally or perfectly
inelastic collision. They are inclined to think of inelasticity as
imperfection, so the idea of perfect imperfection is distressing.
Consequently the scale shifts and they label collisions when objects
stick together as inelastic, the general collision as elastic, and
collisions conserving kinetic energy as perfectly elastic.
Questions to Reveal Student Reasoning
How fast would the car have to be traveling for the combined vehicles to
remain at rest after the collision?
If the collision was elastic, in which direction would the sports car
travel after the collision?
Suggestions
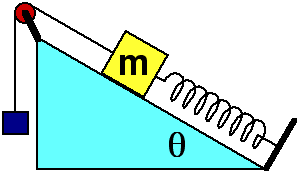
By relating the general collision problem to that of two masses
colliding with a spring between them, it is possible to get students to
realize that all two body collisions pass through the state with both
objects traveling with the CM velocity. This helps unify the concepts
of elastic, inelastic and perfectly inelastic collisions.