Goal: Problem solving
Source: UMPERG-ctqpe23
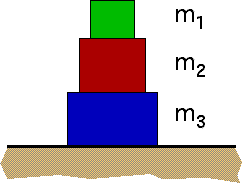
If m2 = 2m1 , m3 = 3m1 and
the force that the surface exerts on the bottom block is 120N, the mass
of the large block is
Use g = 10 N/kg.
- 2 kg
- 4 kg
- 6 kg
- 8 kg
- 12 kg
- 20 kg
- none of the above
Goal: Problem solving
Source: UMPERG-ctqpe23

If m2 = 2m1 , m3 = 3m1 and
the force that the surface exerts on the bottom block is 120N, the mass
of the large block is
Use g = 10 N/kg.
Goal: Problem solving with dynamics
Source: UMPERG-ctqpe21
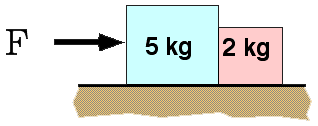
Two blocks rest on a frictionless surface. Both blocks move to the right
with acceleration of 2 m/s2. The force on the big block due
to the small block is
(7) The force on the small block must cause the specified acceleration.
The 3rd law requires that the force on the big block be equal and
opposite. The magnitude is 4N but it is directed to the left.
Goal: Reason with the concept of moment of inertia
Source: UMPERG-ctqpe116
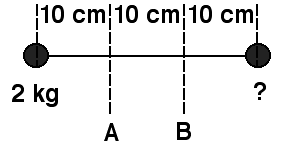
The rotational inertia of the dumbbell (see figure) about axis A is
twice the rotational inertia about axis B. The unknown mass is
(4) Students can get bogged down in calculations when it is unnecessary
to do detailed calculations. Proportional distances to the axes is all
that is needed. This problem presents a good opportunity to discuss
problem solving procedures.
Goal: Problem solving with rotational kinematics
Source: UMPERG-ctqpe110
A flywheel rotating about an axis through its center starts from rest,
rotates with constant angular acceleration for 2 seconds while making
one complete revolution and thereafter maintains constant angular
velocity. How long does it take the wheel to make a total of 6 full
revolutions?
(4) This problem provides an excellent opportunity to discuss the power
of graphs for problem solving. Making a sketch of angular velocity vs.
time provides the easiest way to answer the problem. Conversely, an
algebraic solution is complicated.
Goal: Hone rotational dynamics
Source: UMPERG-ctqpe1246
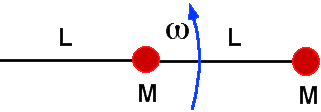
A system consisting of two masses on a string is rotating with angular
velocity ω on a frictionless horizontal surface. The center of
rotation is the left-hand side of the string (nailed to the table).
The ratio of the tension in the inner string to that in the outer string
is
(3) Many students think the ratio is determined just by the string
lengths and give as an answer either (2) or (4). They fail to draw a
free body diagram for the inner mass and, consequently, fail to realize
that it is the net force on the inner mass that must maintain the
circular motion of the inner mass.
Goal: Problem solving
Source: UMPERG-ctqpe147
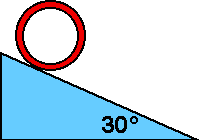
A hoop of mass 4 kg and radius r rolls
without slipping down an incline 30° to the horizontal. The hoop is
released from rest. What is the speed of the hoop after its center has
fallen a distance h?
(3.) Students should realize that the speed cannot depend upon the
radius. Answer #2 is the speed that a falling point mass would have and
the hoop must have less than that.
Goal: Reason with rotational dynamics.
Source: UMPERG-ctqpe138
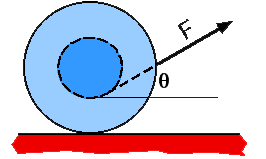
A spool has string wrapped around its center axle and is sitting on a
horizontal surface. If the string is pulled at an angle to the
horizontal when drawn from the bottom of the axle, the spool will
(4) The motion of the spool depends upon the angle θ. When the line of
action of the force passes through the contact point the spool will
slide and not rotate. At lower angles it will roll to the right and at
higher angles it will roll to the left.
Goal: Hone the concept of torque
Source: UMPERG-ctqpe131
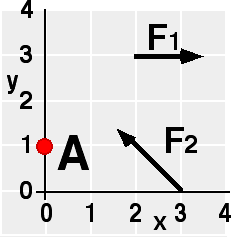
Which of the following statements is true about this situation?
(3) Many students realize that there is at least one point, the
intersection of the lines of action of the two forces, having zero
torque. A drawing is usually sufficient to convince students that there
is an entire line along which the torque is zero.
Goal: Reason with rotational dynamics.
Source: UMPERG-ctqpe136
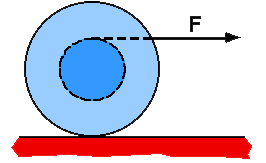
A spool has string wrapped around its center axle and is sitting on a
horizontal surface. If the string is pulled in the horizontal direction
when tangent to the top of the axle, the spool will
(1) For many students this remains counterintuitive.
Goal: Reasoning about work and energy.
Source: UMPERG-ctqpe72
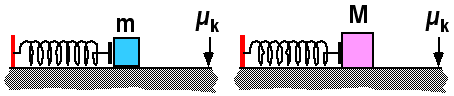
Consider the two situations shown above. The springs are identical and
are compressed the same amount, but the masses are different with M > m.
The surfaces they sit on have the same non-zero coefficient of friction.
Both start from rest. Which mass has the largest speed when the spring
reaches its relaxed length?
(1) Friction is only a confounding element. The lighter mass will have
the greater speed whether or not there is friction.
Students may correctly reason that the friction force will be less on m
and less of the potential energy stored in the spring will be dissipated
as the spring returns to its relaxed length. While true this is not
relevant for the question.
This is an instance where it is important to elicit student reasoning.
It is a case where students can use wrong reasoning to get the correct
answer.
Commentary:
Answer
(3) the most common other answers are #1 and #6, each of which
represents a typical mistake students make. This problem presents a good
opportunity to encourage students to check their answer.