Goal: Reasoning about forces and torques.
Source: UMPERG-ctqpe158
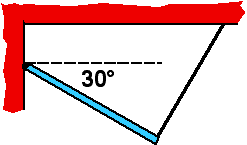
A uniform rod is hinged to a wall and held at a 30° angle by a thin
string that is attached to the ceiling and makes a 90° angle to rod.
Which statement must be true?
Goal: Hone the concept of torque.
Source: UMPERG-ctqpe150
A uniform rod of length L, mass M, is suspended by two thin strings.
Which of the following statements is true regarding the tensions in the
strings?
(3) The ratio is most easily found by considering torques about the
center of the bar. The distances of the strings to the center of the
bar need to be determined visually from the figure.
Goal: Reasoning with forces
Source: UMPERG-ctqpe154
A uniform rod of length 4L, mass M, is suspended by two thin strings,
lengths L and 2L as shown. What is the tension in the string at the
left end of the rod?
(2) For many this is straightforward but a few students are confused
about the effect of the unequal lengths of string.
Goal: Problem solving
Source: UMPERG-ctqpe166
A uniform disk with mass M and radius R sits at rest on an incline
30° to the horizontal. A string is wound around disk and attached
to top of incline as shown. The string is parallel to incline. The
friction force acting at the contact point is:
(3) Balancing torques about the center of the disk determines that the
friction force points up and is equal to the tension in the string. (The
other forces, gravity and normal pass through the point and contribute
no torques.) Balancing torques about the contact point determines the
tension readily.
Goal: Problem solving
Source: UMPERG-ctqpe162
A uniform disk with R=0.2m rolls without slipping on a horizontal
surface. The string is pulled in the horizontal direction with force
15N. The disk’s moment of inertia is 0.4 kg-m2. The friction
force on the disk is:
(4) This problem can be done without the arithmetic complication of
finding the mass from the center-of-mass moment of inertia. This is an
excellent problem for stressing multiple solution methods. This is a
situation where two equations are needed. They can be either the linear
dynamical relation and a rotational dynamical relation, or just two
rotational relationships about different points. Some students may
answer (7) because they are unfamiliar with the expression for moment of
inertia about the CM or because they do not know the Parallel Axis
theorem.
Goal: Problem Solving
Source: UMPERG-ctqpe164
A uniform disk with mass M and radius R sits at rest on an incline
30° to the horizontal. String is wound around disk and attached to
top of incline as shown. The string is parallel to incline. The
tension in the string is :
(4) This problem can be solved a variety of ways. The simplest method is
to balance torques about the contact point. This situation is an
excellent one for discussing the advantages of thinking about preferred
points about which to write the rotational dynamics equation.
Goal: Problem solving
Source: UMPERG-ctqpe88
Two blocks, M=2m, sit on a horizontal frictionless surface with a
compressed massless spring between them. After the spring is released
M has velocity v. The total energy initially stored in the spring was:
(3) The big mass has kinetic energy mv2 and the small mass
has energy 2mv2. Some students may answer (6) because they
have confused M and m. It is important to determine the reasons that
any student might select (7). They might be unwilling to assume that
the system is initially at rest. Students taking this perspective
should not be disconfirmed but congratulated for making a critical
interpretation of the wording.
Goal: Hone angular kinematic quantities and distinguish them from linear kinematic quantities.
Source: UMPERG
A mass moves in a circle with uniformly increasing anglular velocity.
As the angular velocity ω increases, the linear acceleration of
the mass has…
(4) This requires exploration. Some students may think that the
direction is changing because the acceleration points toward the center
of the circle. They may be unaware that there is also a component of the
acceleration in the tangential direction.
Some students may answer (3) thinking only of the radial acceleration
and that ‘towards the center’ is a direction.
Goal: Hone angular kinematic quantities and distinguish them from linear kinematic quantities.
Source: UMPERG
A mass moves in a circle with uniformly increasing angle.
As the angle θ increases, the linear acceleration of the mass has
…
(2) Students have a lot of difficulty reconciling linear kinematics with
angular kinematics. Unless shown how to take derivatives in polar
coordinates, or shown how to represent rotational kinematic quantities
as vectors, students can only memorize specific relationships.
Some students may answer (1) thinking that ‘towards the center’ is a
direction.
Goal: Reasoning and recognizing the implications of momentum conservation.
Source: UMPERG
For ANY collision between two objects there is a time when both of the
objects are traveling with the velocity of the center of mass.
(Assume no external forces act on either object.)
(2) This statement is false despite the fact that it is true for just
about all of the instances of collision that students see. In a
perfectly inelastic collision it is certainly true that both bodies have
the velocity of the center of mass after the collision. In a general one
dimensional collision with only spring forces it is also true. For the
statement to be true about a specific collision, there must be a time
when the relative velocity of the two objects is zero. The statement is
clearly false in general for two-dimensional collisons. As an example of
a one-dimensional collision for which the statement is false, consider a
bullet that passes through a block of wood initially at rest. The bullet
slows down and the block speeds up but they never have the same
velocity.
Commentary:
Answer
(4) This is easily determined by considering torques about the hinge.
The hinge force cannot be purely vertical because there is a horizontal
component to the tension that must be balanced. Also the hinge force
cannot be purely horizontal or the rod would rotate counterclockwise
about its center. Since the hinge force must have a horizontal component
in the opposite direction as the horizontal component of the tension,
(3) cannot be true either.