Goal: Reasoning with dynamics.
Source: UMPERG
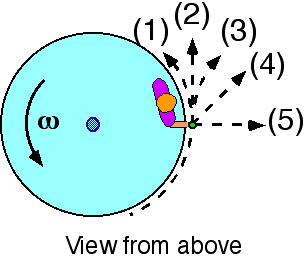
A child stands on a spinning disk. Suppose that there is friction
between the child’s shoes and the surface of the disk. While holding a
rock the child stands at the largest radius possible for the current
angular velocity without slipping. After releasing the rock, the child
will…
Goal: Reasoning with dynamics.
Source: UMPERG
Two masses (M > m) are on an incline. Both surfaces have the same
coefficient of kinetic friction. Both objects start from rest, at the
same height. Which mass has the largest speed at the bottom?
(3) Both will have the same speed. All the forces acting on the mass
(normal, friction, gravity) are proportional to the mass so the mass
cannot affect the acceleration experienced by the mass.
Goal: Problem solving
Source: UMPERG
A bug sits on a disk at a point 0.5 m from the center. If the
coefficient of friction between the bug and disk is 0.8, the maximum
angular velocity the disk can have before the bug slips off the disk is
most nearly:
(2) Some students may respond (6) thinking that the mass of the bug is
needed for solution.
Goal: Problem solving using conservation of angular momentum.
Source: UMPERG
A bug walks on a freely rotating disk. Given: Mbug=0.05 kg,
Idisk=0.03 kg-m2, Rdisk=0.5 m, and
ωo= 2 rad/s when bug is 0.1 m from center. The bug
crawls to 0.4 m from the disk’s center. The final ω is most
nearly:
(1) This is a very traditional conservation of angular momentum problem.
The only difficulty is due to the presence of extraneous information.
Some students may use conservation of energy.
Goal: Develop a strategic approach to problem solving.
Source: UMPERG
A bug walks on a rotating disk. Given: Mbug,
Idisk, Rdisk, and ωo when the bug
is at r1. The bug crawls to r2. Find
ωfinal for the system.
What principle would you use to solve the problem MOST EFFICIENTLY?
(5) This problem helps students develop a principle-based approach to
problems. Many students may think correctly that this is a conservation
of angular momentum problem and not recognize that the general principle
is the angular impulse – angular momentum theorem.
Goal: Distinguish average velocity from velocity.
Source: UMPERG
A car is initially located at the 109 mile marker on a long straight
highway. Two and one half minutes later the car is located at the 111
mile marker.
What is the velocity of the car?
The correct answer is (7) because only the average velocity can be
determined. However, students who respond (4) should not be
disconfirmed but prodded to be more discriminating when interpreting
questions. They have assumed that the car is traveling with a uniform
speed.
Students should be able to extract kinematical quantities from everyday
situations. They should also have a sense of the size of these
quantities.
What is the speed of the car when it is at the 109 mile marker? How do
you know?
Is it possible for the car to be at rest initially and reach the 111
mile marker two and one half minutes later? If it had constant
acceleration, what would its speed be when it reached the 111 mile
marker?
Have students make a sketch of position vs. time. They probably assume
that the speed is uniform throughout the time interval. Have them
consider other paths that still connect the two known points on the
position vs. time plot. Draw some reasonable path and have the students
describe what the car is doing during that interval.
Goal: Hone the concepts of speed and velocity.
Source: UMPERG
The radius of the Earth is 6,400 km. The speed and direction would you
have to travel along the equator to make the sun appear fixed in the sky
is most nearly
(8) You would attempt to remain underneath the sun as it traveled from
East to West. Some students may be confused by the tilt of the Earth’s
axis and think that the Sun could not remain fixed in the sky if you
were constrained to move along the equator. These students would likely
answer (9).
Students should be able to determine the speed and direction even if
they do not yet have a solid grasp of velocity as a vector.
What is the circumference of the Earth? Does everyone on the Earth
travel at the same speed?
Build a simple model. Most students can readily grasp the result when
the Earth’s axis is perpendicular to the plane of the Earth’s orbit. A
model helps them understand that the tilt of the axis doesn’t matter.
Goal: Interrelate and contrast the concepts of work, kinetic energy and impulse.
Source: UMPERG-ctqpe96
Compare two collisions that are perfectly inelastic. In case (A) a car
traveling with velocity V collides head-on with a sports car having half
the mass and traveling in the opposite direction with twice the speed.
In case (B) a car traveling with velocity V collides head-on with a
light truck having twice the mass and traveling in the opposite
direction with half the speed. In which case is the work done on the
car during the collision the greatest?
(4) The total momentum of both systems is zero, so after the collision
there is no KE in either system. System (A) has more kinetic energy
initially. There is no way, however, to determine how much of the
kinetic energy in the combined system of the two vehicles is dissipated
in the automobile as opposed to the other vehicle.
This question serves only to provoke a discussion of the dissipation of
energy in a collision. Students are tempted to assume that each
vehicle must absorb its own initial KE.
How do the forces acting on the car in the two cases compare?
Which collision takes longer?
Which vehicle do you think will suffer the greatest damage?
Promote a discussion of auto safety.
Goal: Contrast the concepts of impulse and work.
Source: UMPERG-ctqpe127
Consider the following statements:
A. If an object receives an impulse, its kinetic energy must change.
B. An object’s kinetic energy can change without it receiving any impulse.
C. An object can receive a net impulse without any work being done on it.
D. A force may do work on an object without delivering any impulse.
Which of the following responses is most appropriate?
(4) We consider only a simple object with no internal structure. A mass
traveling in a circle with constant speed (mass on a string, satellite
in circular orbit or marble rolling around a hoop on a horizontal
surface) receives a net impulse, say, every quarter circle without any
work being done because the force is perpendicular to the motion.
Students need to sort out the difference between impulse (integral of
force over time) and work (integral of force over displacement). This
question is most easily answered considering the impulse-momentum
theorem and the work-kinetic energy theorem. The example mentioned in
the answer to demonstrate the truth of statement C also serves to
demonstrate the falseness of statement A. As for statement B, if an
object’s KE changes its momentum must change so it must have received an
impulse. Statement D is also false because if a force does work on the
object it must have acted over time.
A book sits at rest on a table. Does gravity do work on the book? Does
gravity provide an impulse?
Compare a satellite in circular orbit around the Earth with a simple
pendulum. Does gravity deliver an impulse over a quarter cycle? a half
cycle? a whole cycle? Does gravity do work on the object over a quarter
cycle? a half cycle? a whole cycle?
Ask students to create physical situations meeting certain
specifications. E.g. A situation for which a force acts over a
particular time causing a change of momentum but no change in kinetic
energy (mass on a spring).
Goal: Hone the concept of impulse and recognize an application of the 3rd law.
Source: UMPERG-ctqpe92
Compare two collisions that are perfectly inelastic. In case (A) a car
traveling with velocity V collides head-on with a sports car having half
the mass and traveling in the opposite direction with twice the speed.
In case (B) a car traveling with velocity V collides head-on with a
light truck having twice the mass and traveling in the opposite
direction with half the speed. In which case is the impulse delivered
to the car during the collision the greatest?
(3) The impulse delivered to the automobile is the same in both cases.
In both cases the initial momentum of the automobile is MV to the right
and the final momentum is zero.
Impulse is related to the change in momentum. This question provided the
opportunity to discuss the definition of impulse [integral of force over
time interval] and its relation to momentum change. Many students think
I=Δp is the definition of impulse rather than the result of Newton’s
second law. Students should realize that no statement can be made about
the forces exerted on the two cars – only that the integral of the force
over the collision time is the same.
How do the forces acting on the car in the two cases compare? Which
collision takes longer?
Set up the comparison with collision carts.
Commentary:
Answer
(4) There should be no consequence of dropping the rock. Because the
normal force changes, so does the friction force. The new friction force
is still able to provide the necessary centripetal force for the
circular motion.