Goal: Reasoning using the 2nd law.
Source: UMPERG
A tow truck (2,000kg) pushing a car (1000kg) experiences an average
friction force of 13,000N while accelerating from rest to a final
velocity of 36 mi/hr (16 m/s). The air and the road exert an average
resistive force of 1,000N on the car. What force does the car exert on
the tow truck?
Goal: Develop good problem solving practices. Determining the value of procedure forces, those requiring use of the 2nd law.
Source: UMPERG
A child is walking along the sidewalk at a constant speed of 1 m/s while
pulling his dog sitting in a wagon. The dog has a mass of 30kg and the
wagon weighs 50N. If the child pulls the wagon with a force of 60N at an
angle of 30°, what is the frictional force exerted by the wagon on
the dog?
(1) The dog is moving at a constant speed, presumably in a straight
line. The net force on the dog must be zero. Since there are no other
possible horizontal forces (if we ignore air resistance) other than the
friction force, the friction force must be zero.
This problem provides students with a lot of information. The challenge
of the problem (and most real problems) is to come to an understanding
of the situation independent of the specific details. Then based on an
understanding of the situation one can attempt to address specific
questions and make use of detailed information.
Ask students to describe the situation. Ask them to describe how they
approached the problem. Did you describe all the forces? Did you draw
any free-body diagrams?
Have students draw a free-body diagram (drawing all possible forces) for
the dog. Have them describe the motion for the dog. Ask them to
re-answer the question.
Goal: Analyze and evaluate a solution to a given problem.
Source: UMPERG
A skateboarder heads straight up a steep bank angled at 45°, the whole time experiencing a constant acceleration. She manages to move 1.6m up the incline before rolling back down. The entire maneuver takes her 1.8 s, half of which is going up, the other half going down. What magnitude acceleration did she experience while on the incline?
Consider the steps in the following procedure. If the procedure is incorrect, respond with the number of the first incorrect step; if not, respond with step 7.
(1) The graph does not describe the situation. The acceleration is constant. The velocity is not zero at t=0s, but is zero at t=.9s.
This question requires students to make decisions and judgements which are needed when solving kinematics problems with understanding. This provides another opportunity to check students skills interpreting graphs and connecting the graph to the physical situation. Students may still be looking at superficial features of the graph to determine its validity.
Where is the skateboarder’s velocity zero? … velocity largest? Does this information match the graph?
What is her initial position? … her final position? Does this information match the graph?
Write out the appropriate solution plan. Ask students to compare the answers for the two approaches. Does an invalid plan necessarily lead to an incorrect answer? Why or why not? Does a valid plan necessarily lead to a correct answer? Why or why not?
Goal: Analyze and evaluate a solution to a given problem.
Source: UMPERG
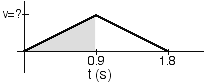
An airplane accelerates down a runway in order to take off
but aborts and applies brakes causing the plane to stop. The plane
speeds up at a constant rate for 5 seconds, then slows down at the same
rate when the brakes are applied. The plane stops at a point that is
100 meters from its initial position. What was the acceleration of the
airplane during the first 5 seconds?
(A) The acceleration of the plane is constant and the same for the
entire motion.
(B) The entire process takes 10 seconds and the displacement is 100
meters.
(C) It is possible, therefore, to use the formula “change in x =
vo,x t + 1/2 ax t2“, where
vo,x is zero and t = 10s.
(D) The only unknown in this equation is ax, so solve for it.
Which of the following is true?
(5) More than one statement is incorrect. The
acceleration is not constant for the entire motion and so (A) is
incorrect. Although the magnitude of the acceleration is constant its
direction changes. Statement (C) is incorrect because the formula in
(C) is only valid over periods the acceleration is constant.
This question requires students to make decisions and judgements which
are needed when solving kinematics problems with understanding. The
kinematics equations are of limited use. They apply directly only to
problems involving constant acceleration. Students are usually not
aware of this limitation and are apt to apply the kinematics expressions
much too broadly. Students also tend to view acceleration as a scalar
quantity and therefore see the acceleration as constant even when it is
not so.
How do we determine the acceleration. What is the acceleration while
the plane is speeding up? … slowing down? If necessary ask the
following. What is the direction of acceleration while the plane is
speeding up? … slowing down?
Draw a graph of velocity vs. time for constant acceleration. Draw a
graph of velocity vs. time for the problem situation. Discuss the
acceleration and displacement in terms of these graphs.
Commentary:
Answer
(4) The net force on the car and tow truck is 12,000N (13,000N –
1,000N). The acceleration is 4m/s2. The magnitude of the force between
the two vehicles is 5,000N.
Background
Answers are not as important as approach. What did students do to
understand the physical situation? Did they draw pictures. Did they
draw a free-body diagram.
Questions to Reveal Student Reasoning
Ask a couple of students to describe how they approached the problem.
Ask them to describe the steps they took without getting into
mathematical details. For example, did they draw a free-body diagram?
What forces did they consider? What system did they analyze?
Suggestions
After a couple of descriptions of how to approach solving the problem,
work through the problem with help from the class.