Goal: Analyze and evaluate a solution to a given problem.
Source: UMPERG
A skateboarder heads straight up a steep bank angled at 45°, the whole time experiencing a constant acceleration. She manages to move 1.6m up the incline before rolling back down. The entire maneuver takes her 1.8 s, half of which is going up, the other half going down. What magnitude acceleration did she experience while on the incline?
Consider the steps in the following procedure. If the procedure is incorrect, respond with the number of the first incorrect step; if not, respond with step 7.
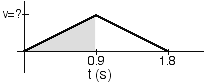
- The velocity vs. time graph for the situation is as shown.
- It takes the skateboarder 0.9 s to reach the highest point.
- The shaded area of the graph equals her displacement along the incline which is 1.6m.
- Equate this area (1/2 (0.9)v) to 1.6 and solve for v.
- Use v to find the slope of the velocity vs. time graph.
- The slope is equal to the acceleration.
- The procedure is correct.
Commentary:
Answer
(1) The graph does not describe the situation. The acceleration is constant. The velocity is not zero at t=0s, but is zero at t=.9s.
Background
This question requires students to make decisions and judgements which are needed when solving kinematics problems with understanding. This provides another opportunity to check students skills interpreting graphs and connecting the graph to the physical situation. Students may still be looking at superficial features of the graph to determine its validity.
Questions to Reveal Student Reasoning
Where is the skateboarder’s velocity zero? … velocity largest? Does this information match the graph?
What is her initial position? … her final position? Does this information match the graph?
Suggestions
Write out the appropriate solution plan. Ask students to compare the answers for the two approaches. Does an invalid plan necessarily lead to an incorrect answer? Why or why not? Does a valid plan necessarily lead to a correct answer? Why or why not?